Question

18．如图，边长为1的正方形ABCD的对角线交于点O，现有半径足够大的扇形OEF且∠EOF=90°，当扇形OEF绕点O转动，扇形OEF和正方形ABCD重叠部分的面积大小的规律是扇形OEF和正方形ABCD重叠部分的面积=$\frac{1}{4}$S_{正方形ABCD}．

Answer 1

分析 根据四边形ABCD为正方形，得到∠OAG=∠OBH=45°，OA=OB，∠AOB=90°；推出△AOG≌△BOH，于是得到结论．

解答 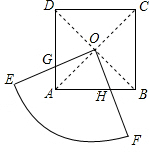解：∵四边形ABCD为正方形，
∴∠OAG=∠OBH=45°，OA=OB，∠AOB=90°；
由题意得：∠GOH=90°，
∴∠AOG=∠BOH；
在△AOG与△BOH中，
$\left\{\begin{array}{l}{∠AOG=∠BOH}\\{OA=OB}\\{∠OAG=∠OBH}\end{array}\right.$，
∴△AOG≌△BOH（ASA），
∴扇形OEF和正方形ABCD重叠部分的面积=S_△AOB=$\frac{1}{4}$S_{正方形ABCD}．
故答案为：扇形OEF和正方形ABCD重叠部分的面积=$\frac{1}{4}$S_{正方形ABCD}．

点评 本题考查了全等三角形的判定和性质，正方形的性质，熟练掌握全等三角形的判定和性质是解题的关键．