题目内容
14.已知$\frac{A}{x+1}$-$\frac{B}{x-3}$=$\frac{x+5}{(x+1)(x-3)}$(其中A,B为常数),求A2014B=-2.分析 根据分式的加减运算法则列出关于A、B的方程组即可求出A、B的值.
解答 解:$\frac{A}{x+1}$-$\frac{B}{x-3}$=$\frac{A(x-3)-B(x+1)}{(x+1)(x-3)}$=$\frac{(A-B)x-3A-B}{(x+1)(x-3)}$
∴$\left\{\begin{array}{l}{A-B=1}\\{-3A-B=5}\end{array}\right.$
解得:$\left\{\begin{array}{l}{A=-1}\\{B=-2}\end{array}\right.$
∴原式=(-1)2014×(-2)=-2
故答案为:-2
点评 本题考查分式的加减法,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.为测量底面为圆形的古塔的高度,以下是小明与小红的研究报告:
(1)写出小明的研究报告中“数据处理”的详细过程;
(2)指出小红研究报告中的错误之处;
(3)利用两人的测量数据,直接写出古塔底面圆的半径(结果精确到1m).
| 小明的研究报告 | 小红的研究报告 | |
| 测量图例 | 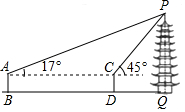 | 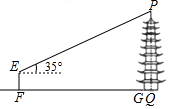 |
| 测量过程 | 如图,测角仪AB、CD的高度均为1.6m,分别测得古塔顶端的仰角为17°、45°,测角仪底端的距离(BD)为69m. | 如图,测角仪EF的高度为1.6m,测得古塔顶端的仰角为35°,测角仪所在位置与古塔底部边缘的最短距离(FG)为38.3m. |
| 参考数据 | sin17°≈0.29,cos17°≈0.96, tan17°≈0.31,$\sqrt{2}$≈1.41 | sin35°≈0.57,cos35°≈0.82, tan35°≈0.70 |
| 数据处理 | 32.6 | PQ=38.3×tan35°+1.6≈28.41(m) |
(2)指出小红研究报告中的错误之处;
(3)利用两人的测量数据,直接写出古塔底面圆的半径(结果精确到1m).
2.“端午节”是中华民族古老的传统节日.甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案.
甲超市方案:购买该种粽子超过200元后,超出200元的部分按95%收费;
乙超市方案:购买该种粽子超过300元后,超出300元的部分按90%收费.
设某位顾客购买了x元的该种粽子.
(1)补充表格,填写在“横线”上:
(2)当x为何值时?到甲、乙两超市的花费一样.
(3)如果顾客在“端午节”当天购买该种粽子超过300元,那么到哪家超市花费更少?说明理由.
甲超市方案:购买该种粽子超过200元后,超出200元的部分按95%收费;
乙超市方案:购买该种粽子超过300元后,超出300元的部分按90%收费.
设某位顾客购买了x元的该种粽子.
(1)补充表格,填写在“横线”上:
| x (单位:元) | 实际在甲超市的花费 (单位:元) | 实际在乙超市的花费 (单位:元) |
| 0<x≤200 | x | x |
| 200<x≤300 | 200+(x-200)×95%(或10+0.95x) | x |
| x>300 | 200+(x-200)×95%(或10+0.95x) | 300+(x-300)×90%(或30+0.9x) |
(3)如果顾客在“端午节”当天购买该种粽子超过300元,那么到哪家超市花费更少?说明理由.