题目内容
7.用简便方法解下列方程:(1)3(x+1)-$\frac{1}{3}$(x-1)=2(x+1)-$\frac{1}{2}$(x-1);
(2)$\frac{5}{6}$[$\frac{6}{5}$($\frac{2}{3}$x-1)-2]=x-3;
(3)1-$\frac{1}{5}$(x-$\frac{10-2x}{3}$)=$\frac{x}{2}$-$\frac{1}{3}$(3x-$\frac{3-6x}{2}$).
分析 (1)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去括号,去分母,移项合并,把x系数化为1,即可求出解.
解答 解:(1)移项,得3(x+1)-2(x+1)+$\frac{1}{2}$(x-1)-$\frac{1}{3}$(x-1)=0,
合并同类项,得(x+1)+$\frac{1}{6}$(x-1)=0,
去分母,得6x+6+x-1=0,
移项、合并同类项,得7x=-5,
系数化为1,得x=-$\frac{5}{7}$;
(2)去括号,得$\frac{2}{3}$x-1-$\frac{5}{3}$=x-3,
去分母,得2x-3-5=3x-9,
移项、合并同类项,得-x=-1,
系数化为1,得x=1;
(3)去括号,得1-$\frac{1}{5}$x+$\frac{10-2x}{15}$=$\frac{x}{2}$-x+$\frac{3-6x}{6}$,
去分母得:30-6x+20-4x=15x-30x+15-30x,
移项合并得:35x=-35,
解得:x=-1.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 如图所示:残缺的圆形轮片上,弦AB的垂直平分线CD交圆形轮片于点C,垂足为D,解答下列问题:
如图所示:残缺的圆形轮片上,弦AB的垂直平分线CD交圆形轮片于点C,垂足为D,解答下列问题: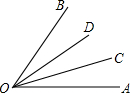 如图所示,如果OC,OD是∠AOB的三等分线,那么∠AOC=∠BOD=∠DOC,∠BOD=$\frac{1}{3}$∠AOB,∠AOD=22∠BOD或2∠DOC或2∠COA.
如图所示,如果OC,OD是∠AOB的三等分线,那么∠AOC=∠BOD=∠DOC,∠BOD=$\frac{1}{3}$∠AOB,∠AOD=22∠BOD或2∠DOC或2∠COA.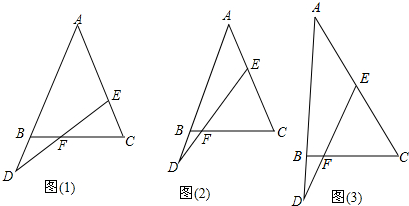
 如图,已知C、D是线段AB上的两点,且AC=$\frac{1}{3}$AB,BD=$\frac{1}{3}$BC,图中一共有6条线段,若AC=3,则CD的长度为4.
如图,已知C、D是线段AB上的两点,且AC=$\frac{1}{3}$AB,BD=$\frac{1}{3}$BC,图中一共有6条线段,若AC=3,则CD的长度为4.