题目内容
19.某商场将进价为20元的某种服装,按60元售出时,每天可以售出20套.据市场调查发现,这种服装每降低1元售价,销量就增加2套,要求售价不得低于成本.(1)求每天销售利润y(元)与售价x(元/件)之间的函数表达式.
(2)当售价为多少时,才能使每天的销售利润最大?最大利润为多少元?
分析 (1)根据每天的销售利润=每件服装的销售利润×销售数量,直接计算即可;
(2)把第(1)小题的解析式化为顶点式,即可解答.
解答 解:(1)由题意得:y=(x-20)[20+2(60-x)],
∴y=-2x2+180x-2800,
(2)∵y=-2x2+180x-2800,
∴y=-2(x-45)2+1250,
∴当x=45时,y最大=1250,
∴当售价为45元时,才能使每天的销售利润最大,最大利润为1250元.
点评 本题主要考查二次函数的应用.能够根据题意,找到等量关系式:每天的销售利润=每件服装的销售利润×销售数量是解决此题的关键,同时要能够熟练的将一般式和顶点式进行转化.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
8.过年了,全班同学每人互发一条短信,共发了45条,设全班有x名同学,列方程为( )
| A. | $\frac{1}{2}x(x-1)=45$ | B. | x(x-1)=45 | C. | x(x+1)=45 | D. | 2x(x-1)=45 |
9.为了促进义务教育办学条件均衡,2015年某市投入4800000元资金为部分学校添置实验仪器及体、音、美器材.4800000这个数用科学记数法表示为( )
| A. | 48×105 | B. | 4.8×106 | C. | 0.48×107 | D. | 4.8×107 |
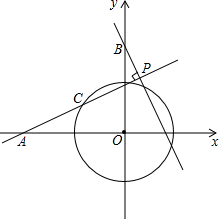 如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为$\frac{1+\sqrt{3}}{2}$cm.
如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为$\frac{1+\sqrt{3}}{2}$cm.