题目内容
11. 完成下面的证明(在括号中注明理由).
完成下面的证明(在括号中注明理由).已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E.
证明:∵BE∥CD(已知),
∴∠2=∠C(两直线平行,同位角相等)
又∵∠A=∠1(已知),
∴AC∥DE(内错角相等,两直线平行),
∴∠2=∠E(两直线平行,内错角相等),
∴∠C=∠E(等量代换)
分析 先根据两直线平行,得出同位角相等,再根据内错角相等,得出两直线平行,进而得出内错角相等,最后根据等量代换得出结论.
解答  证明:∵BE∥CD(已知)
证明:∵BE∥CD(已知)
∴∠2=∠C(两直线平行,同位角相等)
又∵∠A=∠1(已知)
∴AC∥DE(内错角相等,两直线平行)
∴∠2=∠E(两直线平行,内错角相等)
∴∠C=∠E(等量代换)
点评 本题主要考查了平行线的性质,解题时注意区分平行线的性质与平行线的判定的区别,条件与结论不能随意颠倒位置.

练习册系列答案
相关题目
1.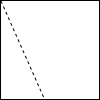 如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
 如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )| A. | 直角三角形 | B. | 平行四边形 | C. | 菱形 | D. | 等腰梯形 |
19.已知两个分式:A=$\frac{4}{{x}^{2}-4}$,B=$\frac{1}{x+2}$+$\frac{1}{2-x}$,其中x≠±2,有下面三个结论:
①A=B;②A•B=1;③A+B=0.
其中正确的有( )
①A=B;②A•B=1;③A+B=0.
其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
1.若a,b为实数,且|a-3|+(b+2)2=0,点P(-a,-b)的坐标是( )
| A. | (-2,3) | B. | (2,-3) | C. | (-3,2) | D. | (-3,-2) |
 如图,已知AB∥CD,∠1=∠2,那么AE与DF平行吗?试说明理由.
如图,已知AB∥CD,∠1=∠2,那么AE与DF平行吗?试说明理由.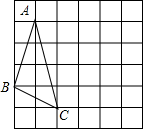 在下面的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分被为(-1,-1),(1,-2),将△ABC绕着点C顺时针旋转90°,则点A的对应点的坐标为(5,-1).
在下面的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分被为(-1,-1),(1,-2),将△ABC绕着点C顺时针旋转90°,则点A的对应点的坐标为(5,-1). 如图,四边形ABCD是矩形纸片,AD=10,CD=8,在CD上取一点E,将纸片沿AE翻折,使点D落在BC边上的点F处.
如图,四边形ABCD是矩形纸片,AD=10,CD=8,在CD上取一点E,将纸片沿AE翻折,使点D落在BC边上的点F处.