题目内容
1. 如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )| A. | 直角三角形 | B. | 平行四边形 | C. | 菱形 | D. | 等腰梯形 |
分析 将剪开的△ABE绕E点旋转180°,EC与EB重合,得到直角三角形;把△ABE平移,使AB与DC重合,则得到平行四边形;把△ABE的顶点E与C重合,B与D重合,与四边形AECD不重叠拼在一起,组成等腰梯形;不能得到菱形;即可得出结论.
解答 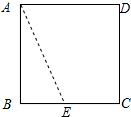 解:将△ABE绕E点旋转180°,EC与EB重合,得到直角三角形,故选项A正确;
解:将△ABE绕E点旋转180°,EC与EB重合,得到直角三角形,故选项A正确;
把△ABE平移,使AB与DC重合,则得到平行四边形,故选项B正确;
把△ABE的顶点E与C重合,B与D重合,与四边形AECD不重叠拼在一起,组成等腰梯形,故选项D正确;
不能得到菱形,故选项C错误.
故选C.
点评 本题考查了图形的剪拼、正方形的性质、平行四边形的判定、等腰梯形的判定等知识;本题难度适中,熟练掌握正方形的性质是解决问题的关键.

练习册系列答案
相关题目
13.教师节来临,某校举办了以感恩为主题的贺卡制作比赛,赛后整理参赛学生的成绩,并制作成如表:
请根据如图表提供的信息解答下列问题:
(1)表中a、b、c所表示的数分别是:a=95,b=90,c=0.3;
(2)参赛学生比赛成绩的中位数落在哪个分数段?求出参赛学生成绩的平均得分;
(3)如果比赛成绩80分以上(含80分)可获得奖励,那么获奖率是多少?
| 分数段/分 | 组中值 | 频数(人数) | 频率 |
| 60≤x<70 | 65 | 30 | 0.15 |
| 70≤x<80 | 75 | b | 0.45 |
| 80≤x<90 | 85 | 60 | c |
| 90≤x<100 | a | 20 | 0.1 |
(1)表中a、b、c所表示的数分别是:a=95,b=90,c=0.3;
(2)参赛学生比赛成绩的中位数落在哪个分数段?求出参赛学生成绩的平均得分;
(3)如果比赛成绩80分以上(含80分)可获得奖励,那么获奖率是多少?
10.已知a>b,若c是任意实数,则下列不等式中总成立的是( )
| A. | a+c<b+c | B. | a-c>b-c | C. | ac<bc | D. | ac>bc |
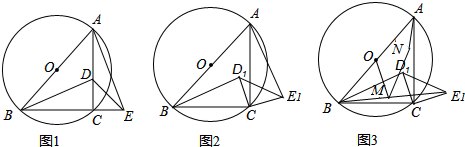
 如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.
如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE. 如图,在等腰△ABC中,AB=AC,点O是△ABC内一点,且OB=OC,联结AO并延长交边BC于点D,如果BD=6,那么BC的值为12.
如图,在等腰△ABC中,AB=AC,点O是△ABC内一点,且OB=OC,联结AO并延长交边BC于点D,如果BD=6,那么BC的值为12. 完成下面的证明(在括号中注明理由).
完成下面的证明(在括号中注明理由).