题目内容
19.已知两个分式:A=$\frac{4}{{x}^{2}-4}$,B=$\frac{1}{x+2}$+$\frac{1}{2-x}$,其中x≠±2,有下面三个结论:①A=B;②A•B=1;③A+B=0.
其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据分式混合运算的法则对各小题进行逐一计算即可.
解答 解:①∵A=$\frac{4}{{x}^{2}-4}$,B=$\frac{1}{x+2}$+$\frac{1}{2-x}$,
∴B=$\frac{1}{x+2}$-$\frac{1}{x-2}$=$\frac{x-2-x-2}{(x+2)(x-2)}$=$\frac{-4}{{x}^{2}-4}$,
∴A≠B,故本小题错误;
②∵A•B=$\frac{4}{{x}^{2}-4}$•($\frac{1}{x+2}$-$\frac{1}{x-2}$)=$\frac{4}{{x}^{2}-4}$•$\frac{-4}{{x}^{2}-4}$=-$\frac{16}{{(x}^{2}-4)^{2}}$,
∴A•B≠1,故本小题错误;
③∵A+B=$\frac{4}{{x}^{2}-4}$+$\frac{-4}{{x}^{2}-4}$=0,
∴A+B=0,故本小题正确.
故选B.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
10.已知a>b,若c是任意实数,则下列不等式中总成立的是( )
| A. | a+c<b+c | B. | a-c>b-c | C. | ac<bc | D. | ac>bc |
7.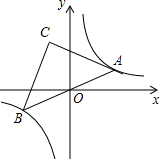 如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
 如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )| A. | y=$\frac{8}{x}$ | B. | y=$\frac{16}{x}$ | C. | y=-$\frac{16}{x}$ | D. | y=-$\frac{8}{x}$ |
14.若点M(x+2,-3)在第三象限,则点N(x,5)的坐标可能为( )
| A. | (0,5) | B. | (2,-3) | C. | (-2,-3) | D. | (-5,5) |
4.已知直线y=kx+b与y=2x-5平行且经过点(1,3),则y=kx+b的表达式是( )
| A. | y=x+2 | B. | y=2x+1 | C. | y=2x+2 | D. | y=2x+3 |
8.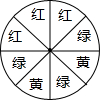 如图是一个可以自由转动的转盘,转动这个转盘后,转出( )色的可能性最小.
如图是一个可以自由转动的转盘,转动这个转盘后,转出( )色的可能性最小.
 如图是一个可以自由转动的转盘,转动这个转盘后,转出( )色的可能性最小.
如图是一个可以自由转动的转盘,转动这个转盘后,转出( )色的可能性最小.| A. | 红 | B. | 黄 | C. | 绿 | D. | 不确定 |
9.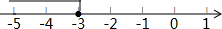 下列不等式中,其解集是如图所示的是( )
下列不等式中,其解集是如图所示的是( )
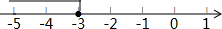 下列不等式中,其解集是如图所示的是( )
下列不等式中,其解集是如图所示的是( )| A. | -x-1≥-2 | B. | -2x-3≥3 | C. | 3x+4≥-5 | D. | x-4≤7 |
 如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.
如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE. 完成下面的证明(在括号中注明理由).
完成下面的证明(在括号中注明理由).