题目内容

2．如图，已知AB∥CD，∠1=∠2，那么AE与DF平行吗？试说明理由．

分析 先根据AB∥CD得出∠BAD=∠CDA，再由∠1=∠2得出∠ADF=∠DAE，由此可得出结论．

解答 解：AE∥DF．
理由：∵AB∥CD，
∴∠BAD=∠CDA（两直线平行，内错角相等），即∠ADF+∠1=∠DAE+∠2．
∵∠1=∠2，
∴∠ADF=∠DAE，
∴AE∥DF（内错角相等，两直线平行）．

点评 本题考查的是平行线的判定与性质，应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．

练习册系列答案
相关题目
12．图1⊙O中，△ABC和△DCE是等腰直角三角形，且△ABC内接于⊙O，∠ACB=∠DCE=90°，连接AE、BD，点D在AC上．

（1）线段AE与BD的数量关系为相等，位置关系为垂直；
（2）如图2若△DCE绕点C逆时针旋转α（0°＜α＜90°），记为△D1CE1；
①当边CE所在直线与⊙O相切时，直接写出α的值；
②求证：AE1=BD1；
（3）如图3，若M是线段BE1的中点，N是线段AD1的中点，求证：MN=$\sqrt{2}$OM．
13．教师节来临，某校举办了以感恩为主题的贺卡制作比赛，赛后整理参赛学生的成绩，并制作成如表：
分数段/分组中值频数（人数）频率
60≤x＜7065300.15
70≤x＜8075b0.45
 80≤x＜908560c
 90≤x＜100a200.1
请根据如图表提供的信息解答下列问题：
（1）表中a、b、c所表示的数分别是：a=95，b=90，c=0.3；
（2）参赛学生比赛成绩的中位数落在哪个分数段？求出参赛学生成绩的平均得分；
（3）如果比赛成绩80分以上（含80分）可获得奖励，那么获奖率是多少？
10．已知a＞b，若c是任意实数，则下列不等式中总成立的是（　　）
A．a+c＜b+cB．a-c＞b-cC．ac＜bcD．ac＞bc
17．在进行二次根式的运算时，如遇到$\frac{2}{\sqrt{3}+1}$这样的式子，还需做进一步的化简：
$\frac{2}{\sqrt{3}+1}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}+1）（\sqrt{3}-1）}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}）^{2}-{1}^{2}}$=$\frac{2（\sqrt{3}-1）}{3-1}$=$\sqrt{3}$-1．
还可以用以下方法化简：
$\frac{2}{\sqrt{3}+1}$=$\frac{3-1}{\sqrt{3}+1}$=$\frac{（\sqrt{3}）^{2}-{1}^{2}}{\sqrt{3}+1}$=$\frac{（\sqrt{3}+1）（\sqrt{3}-1）}{\sqrt{3}+1}$=$\sqrt{3}$-1．
这种化去分母中根号的运算叫分母有理化．
分别用上述两种方法化简：$\frac{2}{\sqrt{5}-\sqrt{3}}$．
7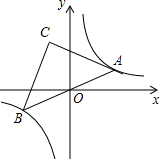．如图，点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰Rt△ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为（　　）
A．y=$\frac{8}{x}$B．y=$\frac{16}{x}$C．y=-$\frac{16}{x}$D．y=-$\frac{8}{x}$
14．若点M（x+2，-3）在第三象限，则点N（x，5）的坐标可能为（　　）
A．（0，5）B．（2，-3）C．（-2，-3）D．（-5，5）
11．完成下面的证明（在括号中注明理由）．
已知：如图，BE∥CD，∠A=∠1，
求证：∠C=∠E．
证明：∵BE∥CD（已知），
∴∠2=∠C（两直线平行，同位角相等）
又∵∠A=∠1（已知），
∴AC∥DE（内错角相等，两直线平行），
∴∠2=∠E（两直线平行，内错角相等），
∴∠C=∠E（等量代换）
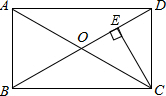12．如图．在矩形ABCD中，对角线AC、BD交于点O，CE⊥BD点E，已知BE：DE=3：1，BD=2$\sqrt{3}$，则矩形ABCD的周长为6+2$\sqrt{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网