题目内容
9.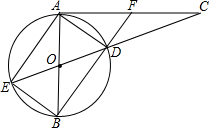 如图AB是半径为R的⊙O的直径,AC是⊙O的切线,其中A为切点.直线OC与⊙O相交于D,E两点,直线BD与AC相交于点F.
如图AB是半径为R的⊙O的直径,AC是⊙O的切线,其中A为切点.直线OC与⊙O相交于D,E两点,直线BD与AC相交于点F.(1)求证:AD•AC=DC•EA
(2)若sin∠CDF=$\frac{\sqrt{3}}{3}$,求线段AC的长.
分析 (1)由AC是⊙O的切线,易得∠CAD=∠AED,又由∠C是公共角,易证得△CAD∽△CEA,然后由相似三角形的对应边成比例,证得结论;
(2)由AB、DE是半径为R的⊙O的直径,证得四边形AEBD是矩形,令∠CDF=θ,可得∠ABD=∠AED=∠FDC=θ,然后由三角函数的性质求得AC的长.
解答 (1)证明:∵AC是⊙O的切线,
∴∠CAD=∠AED,
∵∠C=∠C,
∴△CAD∽△CEA,
∴$\frac{AD}{EA}$=$\frac{DC}{AC}$,
∴AD•AC=DC•EA;
(2)解:∵AB、DE是半径为R的⊙O的直径,
∴AB=DE,OA=OE=OB=OD,
∴四边形AEBD是矩形,
∴AE∥BF,
令∠CDF=θ,则∠ABD=∠AED=∠FDC=θ,
∴sin∠CDF=sinθ=$\frac{\sqrt{3}}{3}$,
∴AD=2Rsinθ=$\frac{2r}{\sqrt{3}}$,AE=BD=2Rcosθ=$\frac{2\sqrt{2}R}{\sqrt{3}}$,
令AC=m,
由(1)可知:CD=$\frac{AD•AC}{EA}$=$\frac{m}{\sqrt{2}}$,
∵CA2=CD•CE=CD(CD+2R),
即m2=$\frac{m}{\sqrt{2}}$(2R+$\frac{m}{\sqrt{2}}$),
解得:AC=m=2$\sqrt{2}$R.
点评 此题考查了相似三角形的判定与性质、切线的性质以及三角函数等知识.注意证得四边形AEBD是矩形,利用三角函数的性质列方程是解此题的关键.

练习册系列答案
相关题目
14.顺次连接对角线相等的任意四边形中点所得的四边形一定是( )
| A. | 梯形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
1.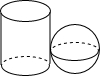 如图,圆柱和球在同一水平面上紧靠在一起组成一个几何体,茗茗画出了它的三视图,其中所画的俯视图应该是( )
如图,圆柱和球在同一水平面上紧靠在一起组成一个几何体,茗茗画出了它的三视图,其中所画的俯视图应该是( )
 如图,圆柱和球在同一水平面上紧靠在一起组成一个几何体,茗茗画出了它的三视图,其中所画的俯视图应该是( )
如图,圆柱和球在同一水平面上紧靠在一起组成一个几何体,茗茗画出了它的三视图,其中所画的俯视图应该是( )| A. | 两个外离的圆 | B. | 两个相交的圆 | C. | 两个外切的圆 | D. | 两个内切的圆 |
18.长春市企业退休人员王大爷2011年的工资是每月2100元,连续两年增长后,2013年大王大爷的工资是每月2541元,若设这两年平均每年的增长率为x,根据题意可列方程( )
| A. | 2100(1+x)=2541 | B. | 2541(1-x)2=2100 | C. | 2100(1+x)2=2541 | D. | 2541(1-x2)=2100 |
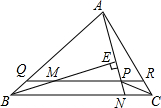 如图,过△ABC的顶点A,作直线AE与∠B的内角平分线垂直相交于点E,且与∠C的内角平分线相交于点P,过P作直线与底边BC平行,且与AB交于Q,与AC交于R,求证:QR=AQ+CR.
如图,过△ABC的顶点A,作直线AE与∠B的内角平分线垂直相交于点E,且与∠C的内角平分线相交于点P,过P作直线与底边BC平行,且与AB交于Q,与AC交于R,求证:QR=AQ+CR.