题目内容
4.计算(1)$\sqrt{(-5)^{2}}$+|1-$\sqrt{2}$|-($\frac{1}{2}$)-2.
(2)25(x+2)2-36=0.
分析 (1)原式利用二次根式性质,绝对值的代数意义,以及负整数指数幂法则计算即可得到结果;
(2)方程整理后,利用平方根定义开方即可求出解.
解答 解:(1)原式=5+$\sqrt{2}$-1-4=$\sqrt{2}$;
(2)方程整理得:(x+2)2=$\frac{36}{25}$,
开方得:x+2=±$\frac{6}{5}$,
解得:x=-$\frac{4}{5}$或x=-$\frac{16}{5}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
16. 如图,△ABC内接于⊙O,且∠ABC=70°,则∠AOC为( )
如图,△ABC内接于⊙O,且∠ABC=70°,则∠AOC为( )
 如图,△ABC内接于⊙O,且∠ABC=70°,则∠AOC为( )
如图,△ABC内接于⊙O,且∠ABC=70°,则∠AOC为( )| A. | 140° | B. | 120° | C. | 90° | D. | 35° |
13.下列各式:$\sqrt{{a}^{2}+{b}^{2}}$,$\sqrt{x+1}$,$\sqrt{{x}^{2}-1}$,$\sqrt{(x-1)^{2}}$,$\sqrt{(-2)^{2}}$,其中是二次根式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.下列长方形中,能使图形不易变形的是( )
| A. |  | B. |  | C. |  | D. |  |
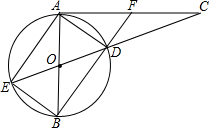 如图AB是半径为R的⊙O的直径,AC是⊙O的切线,其中A为切点.直线OC与⊙O相交于D,E两点,直线BD与AC相交于点F.
如图AB是半径为R的⊙O的直径,AC是⊙O的切线,其中A为切点.直线OC与⊙O相交于D,E两点,直线BD与AC相交于点F.