题目内容
5.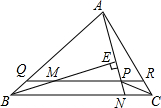 如图,过△ABC的顶点A,作直线AE与∠B的内角平分线垂直相交于点E,且与∠C的内角平分线相交于点P,过P作直线与底边BC平行,且与AB交于Q,与AC交于R,求证:QR=AQ+CR.
如图,过△ABC的顶点A,作直线AE与∠B的内角平分线垂直相交于点E,且与∠C的内角平分线相交于点P,过P作直线与底边BC平行,且与AB交于Q,与AC交于R,求证:QR=AQ+CR.
分析 根据角平分线的定义可得∠ABE=∠CBE,再利用“角边角”证明△ABE和△NBE全等,根据全等三角形对应角相等可得∠BAE=∠BNE,再根据两直线平行,同位角相等可得∠APQ=∠BNE,从而得到∠BAE=∠APQ,然后根据等角对等边可得AQ=PQ,根据角平分线的定义可得∠ACP=∠BCP,根据两直线平行,内错角相等可得∠BCP=∠CPR,从而得到∠ACP=∠CPR,根据等角对等边可得CR=PR,然后根据QR=PQ+PR等量代换即可得证.
解答 证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵BE⊥AN,
∴∠AEB=∠NEB=90°,
在△ABE和△NBE中,$\left\{\begin{array}{l}{∠ABE=∠CBE}\\{BE=BE}\\{∠AEB=∠NEB=90°}\end{array}\right.$,
∴△ABE≌△NBE(ASA)
∴∠BAE=∠BNE,
∵QR∥BC,
∴∠APQ=∠BNE,
∴∠BAE=∠APQ,
∴AQ=PQ,
∵CP平分∠ACB,
∴∠ACP=∠BCP,
∵QR∥BC,
∴∠BCP=∠CPR,
∴∠ACP=∠CPR,
∴CR=PR,
由图可知,QR=PQ+PR,
∴QR=AQ+CR.
点评 本题考查了全等三角形的判定与性质,平行线的性质,等角对等边的性质,熟练掌握三角形全等的判定方法并准确识图是解题的关键.

练习册系列答案
相关题目
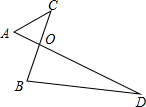 如图,AD与BC相交于点O,$\frac{OA}{OB}$=$\frac{OC}{OD}$,且OA=2,OB=AC=3,求BD的长.
如图,AD与BC相交于点O,$\frac{OA}{OB}$=$\frac{OC}{OD}$,且OA=2,OB=AC=3,求BD的长. 如图,∠AOB=30°,P是∠AOB内一点,PO=5,Q、R分别是OA、OB上的动点,求△PQR周长的最小值5.
如图,∠AOB=30°,P是∠AOB内一点,PO=5,Q、R分别是OA、OB上的动点,求△PQR周长的最小值5.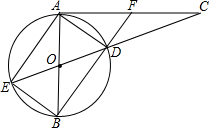 如图AB是半径为R的⊙O的直径,AC是⊙O的切线,其中A为切点.直线OC与⊙O相交于D,E两点,直线BD与AC相交于点F.
如图AB是半径为R的⊙O的直径,AC是⊙O的切线,其中A为切点.直线OC与⊙O相交于D,E两点,直线BD与AC相交于点F.