题目内容
如图,梯形ABCD中,AB∥DC,DE⊥AB,CB⊥AB,且AE = EB = 5,DE = 12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止。设运动时间为t秒,y = S△EPB,则y与t的函数图象大致是【 】

A. B.
B.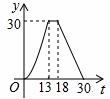 C.
C. D.
D.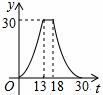
A。
【考点】动点问题的函数图象,直角梯形的性质,勾股定理,锐角三角函数定义,分类思想的应用。
【分析】分三段考虑,①点P在AD上运动,②点P在DC上运动,③点P在BC上运动,分别求出y与t的函数表达式,继而可得出函数图象:
在Rt△ADE中, ,
,
① 点P在AD上运动时,


综上可得选项A的图象符合。故选A。

练习册系列答案
相关题目
 写有数
写有数 字﹣2,﹣1,1的卡片,它们的背面完全相
字﹣2,﹣1,1的卡片,它们的背面完全相 同,将这
同,将这 三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,不放回卡片洗匀,再从余下的两张卡片中随机抽取
三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,不放回卡片洗匀,再从余下的两张卡片中随机抽取 一张,以其正面的数字作为y的值,两次结果记为(x,y)。
一张,以其正面的数字作为y的值,两次结果记为(x,y)。 图或列表法表示(x,y)所有可能出现的结果;
图或列表法表示(x,y)所有可能出现的结果; 无意义的(x,y)
无意义的(x,y)
 的抛物线
的抛物线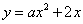
 与
与
 轴相交于点
轴相交于点
 、
、



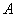
 .点P是
.点P是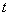
 ,当0<S≤18时,求
,当0<S≤18时,求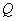
 ,使△OP
,使△OP 到与AB相切于点D的位置,则⊙O自转了【 】
到与AB相切于点D的位置,则⊙O自转了【 】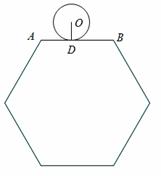
 6,AB=DC=
6,AB=DC=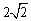 ,若动直线l垂直于BC,且从经过点B的位置向右平移,直至经过点C的位置停止,设扫过的阴影部分的面积为S
,若动直线l垂直于BC,且从经过点B的位置向右平移,直至经过点C的位置停止,设扫过的阴影部分的面积为S ,BP为x,则S关于x的函数关系式是 。
,BP为x,则S关于x的函数关系式是 。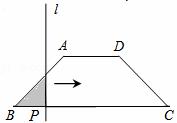
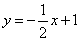
 交坐标轴于
交坐标轴于
 两点,以线段
两点,以线段
 为边向上作正方形
为边向上作正方形
 ,过点
,过点
 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为
 .
.

 出点
出点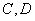
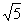
 个单位长度的速度沿射线
个单位长度的速度沿射线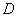
 落在
落在
 轴上时停止.设正方形落在
轴上时停止.设正方形落在
 ,求
,求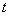
 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量 经过平移得到抛物线
经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积为【 】
,其对称轴与两段抛物线所围成的阴影部分的面积为【 】
 于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积,
于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积,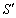
 表
表 示矩形NFQC的面积
示矩形NFQC的面积

 是
是 等腰三角形.
等腰三角形.