题目内容
菱形ABCD中,∠ABC=450,点P是对角线BD上的任一点,点P关于直线AB、AD、CD、BC的对称点分别是点E、F、G、H, BE与DF相交于点M,DG与BH相交于点N,证明:四边形BMDN是正方形。
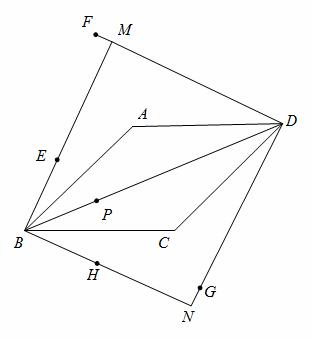
∵四边形ABCD是菱形,
∴∠ABD=∠DBC=∠ADB =∠BDC。
=∠BDC。
∵∠ABC=450,点P关于直线AB、AD、CD、BC的对称点分别是点E、F、G、H,
 ∴∠MBN=∠MDN=900,∠MBC=∠MDB=450。
∴∠MBN=∠MDN=900,∠MBC=∠MDB=450。
∴△BDM是等腰直角三角形。
∴∠BMD=900,BM=DM。
∴四边形BMDN是正方形。
【考点】菱形的性质,轴对称的性质,正方形的判定,等腰直角三角形的判定和性质。


练习册系列答案
相关题目
 bx+1与x轴只有一个交点,且过点A(m,n),B(m+4,n),则n=
bx+1与x轴只有一个交点,且过点A(m,n),B(m+4,n),则n= ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC
ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC 、PF⊥BD,垂足分别为E、F。
、PF⊥BD,垂足分别为E、F。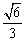 PE,PE=
PE,PE= ,EO=1,求∠EPF的度数;
,EO=1,求∠EPF的度数; -4,求BC的长。
-4,求BC的长。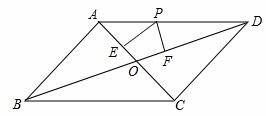
 BD;
BD; EB;
EB; 求阴影部分的面积。
求阴影部分的面积。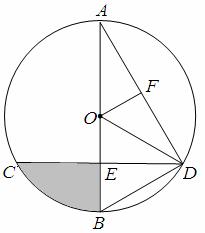


 A;
A; OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m=
OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m= ,点E的坐标为 ;
,点E的坐标为 ;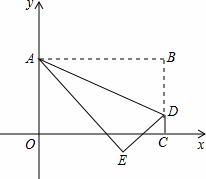
 ,并求出使
,并求出使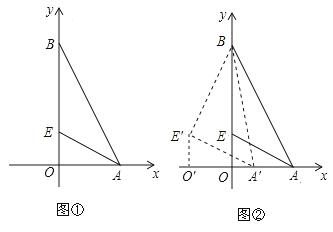

 B.
B.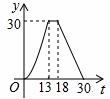 C.
C. D.
D.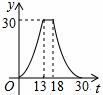
 点A(0,4),B(-3,4),C(-6,0),动点P从点A出发以1个单位/秒的速度在y轴上向下运动,动点Q同时从点C出发以2个单位/秒的速度在x轴上向右运动,过点P作PD⊥y轴,交OB于D,连接DQ.当点P与点O重合时,两动点均停止运动.设运动的时间为t秒.
点A(0,4),B(-3,4),C(-6,0),动点P从点A出发以1个单位/秒的速度在y轴上向下运动,动点Q同时从点C出发以2个单位/秒的速度在x轴上向右运动,过点P作PD⊥y轴,交OB于D,连接DQ.当点P与点O重合时,两动点均停止运动.设运动的时间为t秒.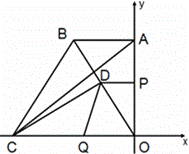

 ABC相似?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
ABC相似?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.