题目内容
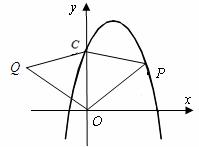
如图,已知直线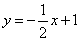
 交坐标轴于
交坐标轴于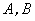
 两点,以线段
两点,以线段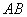
 为边向上作正方形
为边向上作正方形
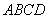
 ,过点
,过点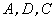
 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为
 .
.

(1)请直接写 出点
出点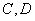
 的坐标;
的坐标;
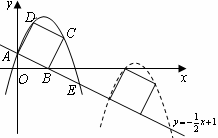
(2)求抛物线的解析式;
(3)若正方形以每秒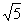
 个单位长度的速度沿射线
个单位长度的速度沿射线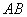
 下滑,直至顶点
下滑,直至顶点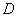
 落在
落在
 轴上时停止.设正方形落在
轴上时停止.设正方形落在
 轴下方部分的面积为
轴下方部分的面积为
 ,求
,求
 关于滑行时间
关于滑行时间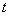
 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量
 的取值范围;
的取值范围;
 1)
1)
 ;(2)
;(2)
 ;
;
(3)当
 时,
时,

当
 时,
时, 




 ;
;
当
 时,
时,
 =
=
 .
.
【解析】


 抛物线过点
抛物线过点


 ,
,



 解得
解得

∴
 ;
;
(3)①当点A运动到点F时,

当
 时,如图1,
时,如图1,


∵
 ,
,

∴

∴

∴
 ;
;
②当点
 运动到
运动到
 轴上时,
轴上时,
 ,
,
当
 时,如图2,
时,如图2,




∴


∴
 ,
,
∵
 ,
,
∴




 ;
;
③当点
 运动到
运动到
 轴上时,
轴上时,
 ,
,
当
 时,如图3,
时,如图3,


∵
 ,
,
∴

∵


 ,
,



 ,
,

 ,
,
∴
 =
=
 .
.
考点:二次函数 的综合题
的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC
ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC 、PF⊥BD,垂足分别为E、F。
、PF⊥BD,垂足分别为E、F。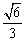 PE,PE=
PE,PE= ,EO=1,求∠EPF的度数;
,EO=1,求∠EPF的度数; -4,求BC的长。
-4,求BC的长。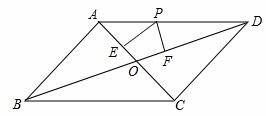
 ,并求出使
,并求出使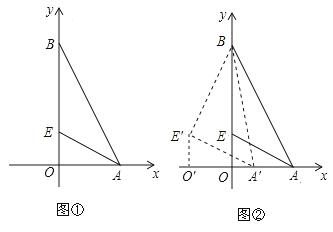

 B.
B.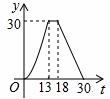 C.
C. D.
D.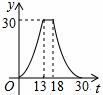
 营O为圆心,半径为4km 圆形考察区域,线段P1、P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整
营O为圆心,半径为4km 圆形考察区域,线段P1、P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整 数)的关系是
数)的关系是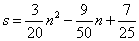
 .以O为原
.以O为原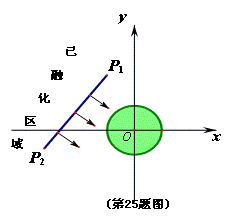

 AF交DP于点A,当点P运动时,
AF交DP于点A,当点P运动时, 在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.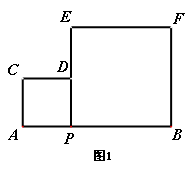

 PQ的中点O所经过的路径的长。
PQ的中点O所经过的路径的长。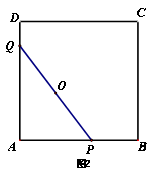




 t为何值时,DQ=2AD?
t为何值时,DQ=2AD?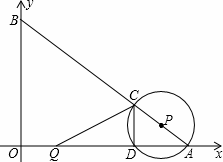
 点A(0,4),B(-3,4),C(-6,0),动点P从点A出发以1个单位/秒的速度在y轴上向下运动,动点Q同时从点C出发以2个单位/秒的速度在x轴上向右运动,过点P作PD⊥y轴,交OB于D,连接DQ.当点P与点O重合时,两动点均停止运动.设运动的时间为t秒.
点A(0,4),B(-3,4),C(-6,0),动点P从点A出发以1个单位/秒的速度在y轴上向下运动,动点Q同时从点C出发以2个单位/秒的速度在x轴上向右运动,过点P作PD⊥y轴,交OB于D,连接DQ.当点P与点O重合时,两动点均停止运动.设运动的时间为t秒.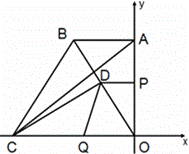

 ABC相似?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
ABC相似?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.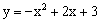 的图象与y轴交于点C,点P是抛物线上的一个动点,点P关于y轴的对称点Q,连接PO,PC,QO,QC,得到四边形
的图象与y轴交于点C,点P是抛物线上的一个动点,点P关于y轴的对称点Q,连接PO,PC,QO,QC,得到四边形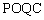 ,是否存在点P,使四边形
,是否存在点P,使四边形