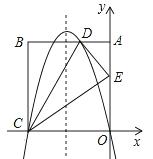
题目内容
如图,对称轴为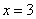
 的抛物线
的抛物线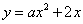
 与
与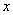
 轴相交于点
轴相交于点
 、
、



(1).求抛物线的解析式,并求出顶点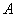
 的坐标
的坐标
(2).连结AB,把AB所在的直线平移,使它经过原点O,得到直线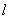
 .点P是
.点P是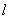
 上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为
上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为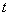
 ,当0<S≤18时,求
,当0<S≤18时,求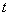
 的取值范围
的取值范围
(3).在(2)的条件下,当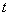
 取最大值时,抛物线上是否存在点
取最大值时,抛物线上是否存在点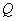
 ,使△OP
,使△OP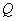
 为直角三角形且OP为直角边.若存在,直接写出点
为直角三角形且OP为直角边.若存在,直接写出点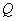
 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(1).(3,3)
(2).-3≤
 <0或0<
<0或0<
 ≤3.
≤3.
(3).存在,点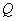
 坐标为(3,3)或(6,0)或(-3,-9)
坐标为(3,3)或(6,0)或(-3,-9)

(说明:可用对称轴为
 ,求
,求
 值,用顶点式求顶点A坐标.)
值,用顶点式求顶点A坐标.)
(2)设直线AB解析式为y=kx+b.
∵A(3,3),B(6,0),
∴
 解得
解得
 , ∴
, ∴
 .
.
∵直线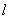
 ∥AB且过点O,
∥AB且过点O,
∴直线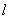
 解析式为
解析式为
 .
.
∵点
 是
是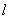
 上一动点且横坐标为
上一动点且横坐标为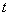
 ,
,
∴点
 坐标为(
坐标为(
 ).
).

作PM⊥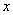
 轴于M,设对称轴与
轴于M,设对称轴与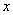
 轴交点为N.
轴交点为N.


则


=-3
 +9.
+9.
∵0<S≤18,
∴0<-3
 +9≤18,
+9≤18,
∴-3≤
 <3.
<3.
又
 <0,
<0,
∴-3≤
 <0.6分
<0.6分


练习册系列答案
相关题目
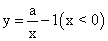 的图象如图,那么关于x的分式方程
的图象如图,那么关于x的分式方程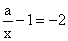 的解是【 】
的解是【 】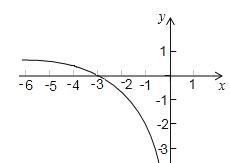
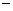 1 B.x=
1 B.x= BD;
BD; EB;
EB; 求阴影部分的面积。
求阴影部分的面积。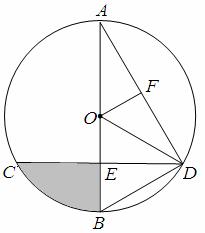
 OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m=
OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m= ,点E的坐标为 ;
,点E的坐标为 ;
 ,并求出使
,并求出使
 旋转45
旋转45 方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;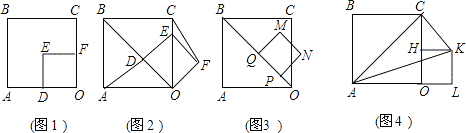


 B.
B.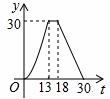 C.
C. D.
D.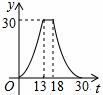
 AF交DP于点A,当点P运动时,
AF交DP于点A,当点P运动时, 在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.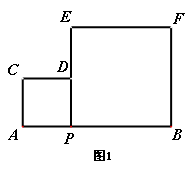

 PQ的中点O所经过的路径的长。
PQ的中点O所经过的路径的长。