题目内容
 如图,在正方形ABCD中,E为AD中点,G为DC上一点,且DG=
如图,在正方形ABCD中,E为AD中点,G为DC上一点,且DG=| 1 |
| 4 |
考点:勾股定理的逆定理,勾股定理
专题:
分析:可设正方形ABCD的边长为a,利用直角三角形中的勾股定理分别求出EG、GF、BE的值,通过EG2+BE2=BG2,可判定BE与EG垂直.
解答:证明:设正方形ABCD的边长为a,再求出Rt△DEG中,EG=
a,
同理求出BE=
a,BG=
a,
∵EG2+BE2=(
a)2+(
a)2=
a2,BG2=(
a)2=
a2,
∴EG2+BE2=BG2,
∴△BEG是直角三角形,
∴BE与EG垂直.
| ||
| 4 |
同理求出BE=
| ||
| 2 |
| 5 |
| 4 |
∵EG2+BE2=(
| ||
| 4 |
| ||
| 2 |
| 25 |
| 16 |
| 5 |
| 4 |
| 25 |
| 16 |
∴EG2+BE2=BG2,
∴△BEG是直角三角形,
∴BE与EG垂直.
点评:主要考查了正方形的性质和直角三角形的判定.会用勾股定理的逆定理判定直角三角形是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知直线l外的两点A、B,且A、B在直线l两旁,则经过A、B两点且圆心在直线l上的圆有( )
| A、0个或1个 |
| B、1个或无数个 |
| C、0个或无数个 |
| D、0个或1个或无数个 |
一个点从数轴上的原点开始,先向右移动4个单位长度,再向左移动5个单位长度,则此时这个点表示的数是( )
| A、0 | B、-2 | C、+1 | D、-1 |
下列每组数中,相等的是( )
| A、53与35 |
| B、-53与(-5)3 |
| C、-54与(-5)4 |
| D、(-5×2)2与-52×22 |
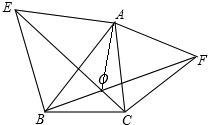 如图,已知△ABC,分别以AB、AC为边作等边△ABE和等边△ACF,BF、CE交于点O.求证:
如图,已知△ABC,分别以AB、AC为边作等边△ABE和等边△ACF,BF、CE交于点O.求证: