题目内容
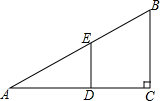 在Rt△ABC中,∠ACB=90°,BC=3,AC=4,D、E分别为AC和AB上的一个动点,则BD+DE的最小值是
在Rt△ABC中,∠ACB=90°,BC=3,AC=4,D、E分别为AC和AB上的一个动点,则BD+DE的最小值是考点:轴对称-最短路线问题
专题:
分析:作点B关于AC的对称点B′,过点B′作B′E⊥AB交AC、AB分别于点D、E,根据轴对称确定最短路线问题,B′E的长度即为BD+DE的最小值,利用勾股定理列式求出AB,再利用∠ABC的正弦列式计算即可得解.
解答: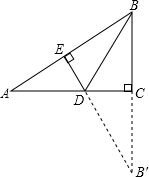 解:如图,作点B关于AC的对称点B′,过点B′作B′E⊥AB交AC、AB分别于点D、E,
解:如图,作点B关于AC的对称点B′,过点B′作B′E⊥AB交AC、AB分别于点D、E,
则B′E的长度即为BD+DE的最小值,BB′=2BC=2×3=6,
∵∠ACB=90°,BC=3,AC=4,
∴AB=
=
=5,
∴B′E=BB′•sin∠ABC=6×
=
,
即BD+DE的最小值是
.
故答案为:
.
 解:如图,作点B关于AC的对称点B′,过点B′作B′E⊥AB交AC、AB分别于点D、E,
解:如图,作点B关于AC的对称点B′,过点B′作B′E⊥AB交AC、AB分别于点D、E,则B′E的长度即为BD+DE的最小值,BB′=2BC=2×3=6,
∵∠ACB=90°,BC=3,AC=4,
∴AB=
| AC2+BC2 |
| 42+32 |
∴B′E=BB′•sin∠ABC=6×
| 4 |
| 5 |
| 24 |
| 5 |
即BD+DE的最小值是
| 24 |
| 5 |
故答案为:
| 24 |
| 5 |
点评:本题考查了利用轴对称确定最短路线问题,主要利用了勾股定理,垂线段最短,锐角三角函数的定义,难点在于确定出点D、E的位置.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
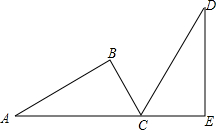 如图,在△ABC中,∠ACB=90°,∠A=30°,把△ABC绕点C旋转一定角度后得到△DEC,点A、C、E在同一直线上,则这个旋转角度为( )
如图,在△ABC中,∠ACB=90°,∠A=30°,把△ABC绕点C旋转一定角度后得到△DEC,点A、C、E在同一直线上,则这个旋转角度为( )| A、60° | B、90° |
| C、120° | D、150° |
一个点从数轴上的原点开始,先向右移动4个单位长度,再向左移动5个单位长度,则此时这个点表示的数是( )
| A、0 | B、-2 | C、+1 | D、-1 |
下列计算错误的是( )
| A、2m+3n=5mn |
| B、(-a2)3=-a6 |
| C、(x2)3=x6 |
| D、a•a2=a3 |
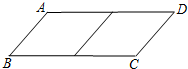 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形.例如:如图,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形.例如:如图,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.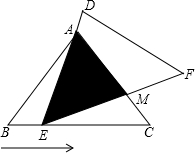 在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.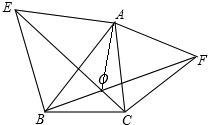 如图,已知△ABC,分别以AB、AC为边作等边△ABE和等边△ACF,BF、CE交于点O.求证:
如图,已知△ABC,分别以AB、AC为边作等边△ABE和等边△ACF,BF、CE交于点O.求证: