Question

15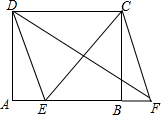．在矩形ABCD中，AD=3，AB=4，点E在线段AB上，将AE平移至BF．
（1）是否存在点E，使得四边形DEFC为菱形？若存在，求出AE长，不存在，说明理由．
（2）直接写出DF、CE、AE之间的数量关系．

Answer 1

分析 （1）由在矩形ABCD中，点E在线段AB上，将AE平移至BF，可得四边形DEFC是平行四边形，又由当DE=CD时，四边形DEFC为菱形，即可求得AE的长；
（2）直接利用勾股定理求解即可求得答案．

解答 解：（1）存在点E，使得四边形DEFC为菱形．
∵四边形ABCD是矩形，
∴∠A=90°，CD=AB=4，CD∥AB，
∵将AE平移至BF，
∴AE=BF，
∴EF=AB，
∴EF=CD，
∴四边形DEFC是平行四边形，
∴当DE=CD=4时，四边形DEFC为菱形，
∴AE=$\sqrt{D{E}^{2}-A{D}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$；

（2）∵四边形ABCD是矩形，
∴∠A=∠ABC=90°，
∴DF²=AD²+AF²=AD²+（2AE+BE）²=AD²+BE²+4AE²+4AE•BE=AD²+CE²-BC²+4AE（AE+BE）=CE²+4AE•AB=CE²+16AE．
∴DF、CE、AE之间的数量关系为：DF²=CE²+16AE．

点评 此题考查了平行四边形的性质、菱形的判定与性质以及勾股定理等知识．注意掌握平移的性质的应用是解此题的关键．