题目内容
9.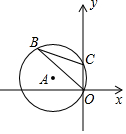 如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )
如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | 2$\sqrt{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2\sqrt{2}}{2}$ |
分析 作直径CD,根据勾股定理求出OD,根据正切的定义求出sin∠CDO,根据圆周角定理得到∠OBC=∠CDO,等量代换即可.
解答 解:作直径CD,
在Rt△OCD中,CD=6,OC=2,
sin∠CDO=$\frac{OC}{CD}$=$\frac{2}{6}$=$\frac{1}{3}$,
由圆周角定理得,∠OBC=∠CDO,
则sin∠OBC=$\frac{1}{3}$,
故选C.
点评 本题考查的是圆周角定理、锐角三角函数的定义,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.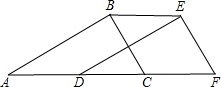 如图,在直角△ABC中,∠ABC=90°,BC=6,AB=8,AC=10,将△ABC沿AC边所在直线向右平移x个单位,记平移后的对应三角形为△DEF,连接BE.当x的值是( )时,S四边形BCEF=24.
如图,在直角△ABC中,∠ABC=90°,BC=6,AB=8,AC=10,将△ABC沿AC边所在直线向右平移x个单位,记平移后的对应三角形为△DEF,连接BE.当x的值是( )时,S四边形BCEF=24.
 如图,在直角△ABC中,∠ABC=90°,BC=6,AB=8,AC=10,将△ABC沿AC边所在直线向右平移x个单位,记平移后的对应三角形为△DEF,连接BE.当x的值是( )时,S四边形BCEF=24.
如图,在直角△ABC中,∠ABC=90°,BC=6,AB=8,AC=10,将△ABC沿AC边所在直线向右平移x个单位,记平移后的对应三角形为△DEF,连接BE.当x的值是( )时,S四边形BCEF=24.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
18.下列说法假命题是( )
| A. | 两直线平行,同位角相等 | B. | 垂线段最短 | ||
| C. | 对顶角相等 | D. | 两点之间直线最短 |
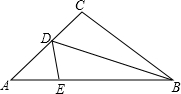 如图所示,三角形纸片ABC,AB=10厘米,BC=7厘米,AC=6厘米.沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为9厘米.
如图所示,三角形纸片ABC,AB=10厘米,BC=7厘米,AC=6厘米.沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为9厘米.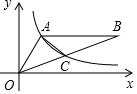 如图,点A(2,3)在反比例函数y=$\frac{k}{x}$(x>0)上,AB∥x轴,连接OB交反比例函数图象于点C,若点C为OB的中点,则S△OAC=4.5.
如图,点A(2,3)在反比例函数y=$\frac{k}{x}$(x>0)上,AB∥x轴,连接OB交反比例函数图象于点C,若点C为OB的中点,则S△OAC=4.5.