题目内容
19.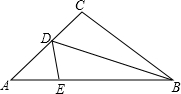 如图所示,三角形纸片ABC,AB=10厘米,BC=7厘米,AC=6厘米.沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为9厘米.
如图所示,三角形纸片ABC,AB=10厘米,BC=7厘米,AC=6厘米.沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为9厘米.
分析 根据翻折变换的性质可得CE=CD,BE=BC=7cm,然后求出AE,再求出AD+DE=AC,最后根据三角形的周长公式列式计算即可得解.
解答 解:∵折叠这个三角形顶点C落在AB边上的点E处,
∴CE=CD,BE=BC=7cm,
∴AE=AB-BE=10-7=3cm,
∵AD+DE=AD+CD=AC=6cm,
∴△AED的周长=6+3=9cm.
故答案为:9.
点评 本题考查了翻折变换的性质,熟记翻折前后的两个图形能够完全重合得到相等的线段是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
10.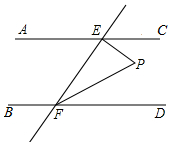 如图,若AC∥BD,EF与AC、BD分别相交于E、F,∠EFD的平分线FP与EP相交于点P.
如图,若AC∥BD,EF与AC、BD分别相交于E、F,∠EFD的平分线FP与EP相交于点P.
(1)探求∠AEF与∠EFP的数量关系并说明理由;
(2)若EP⊥EF,∠AEF=45°,求∠P的度数.
 如图,若AC∥BD,EF与AC、BD分别相交于E、F,∠EFD的平分线FP与EP相交于点P.
如图,若AC∥BD,EF与AC、BD分别相交于E、F,∠EFD的平分线FP与EP相交于点P.(1)探求∠AEF与∠EFP的数量关系并说明理由;
(2)若EP⊥EF,∠AEF=45°,求∠P的度数.
14.圆有( )条对称轴.
| A. | 1 | B. | 2 | C. | 4 | D. | 无数条 |
9.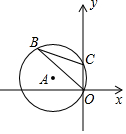 如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )
如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )
 如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )
如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | 2$\sqrt{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2\sqrt{2}}{2}$ |
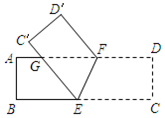 如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=80°,则∠GFD′=20°.
如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=80°,则∠GFD′=20°.