题目内容
20．若关于x的不等式$\left\{\begin{array}{l}{3x-m＜0}\\{7-2x≤1}\end{array}\right.$的整数解共有4个，则m的取值范围18＜m≤21．分析 关键不等式的性质求出不等式的解集，根据找不等式组解集的规律找出不等式组的解集，根据已知得到6≤$\frac{1}{3}$m＜7即可求得．
解答 解：$\left\{\begin{array}{l}{3x-m＜0①}\\{7-2x≤1②}\end{array}\right.$，
由①得：x＜$\frac{1}{3}$m，
由②得：x≥3，
∴不等式组的解集是3≤x＜$\frac{1}{3}$m，
∵关于x的不等式$\left\{\begin{array}{l}{3x-m＜0}\\{7-2x≤1}\end{array}\right.$的整数解共有4个，
∴6＜$\frac{1}{3}$m≤7，
∴18＜m≤21
故答案为：18＜m≤21．
点评 本题主要考查对解一元一次不等式，不等式的性质，解一元一次不等式组，一元一次不等式组的整数解等知识点的理解和掌握，能根据不等式组的解集得到6＜$\frac{1}{3}$m≤7是解此题的关键．
练习册系列答案
相关题目
10．
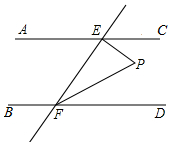如图，若AC∥BD，EF与AC、BD分别相交于E、F，∠EFD的平分线FP与EP相交于点P．
（1）探求∠AEF与∠EFP的数量关系并说明理由；
（2）若EP⊥EF，∠AEF=45°，求∠P的度数．
如图，若AC∥BD，EF与AC、BD分别相交于E、F，∠EFD的平分线FP与EP相交于点P．（1）探求∠AEF与∠EFP的数量关系并说明理由；
（2）若EP⊥EF，∠AEF=45°，求∠P的度数．
12．下列式子一定是二次根式的是（ ）
| A． | $\sqrt{\frac{1}{4}}$ | B． | $\sqrt{x}$ | C． | $\sqrt{x+2}$ | D． | $\sqrt{{x^2}-2}$ |
9．
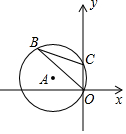如图，在平面直角坐标系中，半径为3的⊙A经过原点O和点C（0，2），若B是y轴左侧⊙A上一点，则sin∠OBC为（ ）
如图，在平面直角坐标系中，半径为3的⊙A经过原点O和点C（0，2），若B是y轴左侧⊙A上一点，则sin∠OBC为（ ）| A． | $\frac{\sqrt{2}}{4}$ | B． | 2$\sqrt{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{2\sqrt{2}}{2}$ |