题目内容
17.(1)计算:$\sqrt{8}$-2sin45°+(2-π)0-($\frac{1}{3}$)-1;(2)化简:(1+$\frac{1}{x-1}$)•$\frac{1}{x}$.
分析 (1)根据特殊角的三角函数值、零指数幂、负整数指数幂可以解答本题;
(2)根据分式的加法和乘法可以解答本题.
解答 解:(1)$\sqrt{8}$-2sin45°+(2-π)0-($\frac{1}{3}$)-1
=$2\sqrt{2}-2×\frac{\sqrt{2}}{2}+1-3$
=$2\sqrt{2}-\sqrt{2}+1-3$
=$\sqrt{2}-2$;
(2)(1+$\frac{1}{x-1}$)•$\frac{1}{x}$
=$(\frac{x-1}{x-1}+\frac{1}{x-1})•\frac{1}{x}$
=$\frac{x}{x-1}•\frac{1}{x}$
=$\frac{1}{x-1}$.
点评 本题考查分式的混合运算、实数的运算、特殊角的三角函数值、零指数幂、负整数指数幂,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
12.下列式子一定是二次根式的是( )
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{x}$ | C. | $\sqrt{x+2}$ | D. | $\sqrt{{x^2}-2}$ |
9.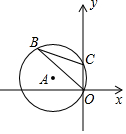 如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )
如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )
 如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )
如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | 2$\sqrt{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2\sqrt{2}}{2}$ |
 如图,把一张长方形纸条ABCD沿EF折叠,若∠1=53°,则∠AEG=74°.
如图,把一张长方形纸条ABCD沿EF折叠,若∠1=53°,则∠AEG=74°.