题目内容
4.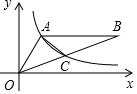 如图,点A(2,3)在反比例函数y=$\frac{k}{x}$(x>0)上,AB∥x轴,连接OB交反比例函数图象于点C,若点C为OB的中点,则S△OAC=4.5.
如图,点A(2,3)在反比例函数y=$\frac{k}{x}$(x>0)上,AB∥x轴,连接OB交反比例函数图象于点C,若点C为OB的中点,则S△OAC=4.5.
分析 先将点A(2,3)代入y=$\frac{k}{x}$,求出反比例函数的解析式,由AB∥x轴及点C为OB的中点,得到点C的纵坐标为1.5,将y=1.5代入反比例函数的解析式求出点C的坐标.作AD⊥x轴于D,CE⊥x轴于E,根据反比例函数系数k的几何意义得出S△OAD=S△OCE,那么S△OAC=S梯形ADEC.
解答 解:将点A(2,3)代入y=$\frac{k}{x}$,得k=2×3=6,
则反比例函数的解析式为y=$\frac{6}{x}$.
∵AB∥x轴,
∴点B的纵坐标于点A的纵坐标相等,都是3,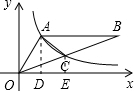 ∵点C为OB的中点,
∵点C为OB的中点,
∴点C的纵坐标为1.5,
将y=1.5代入y=$\frac{6}{x}$,得1.5=$\frac{6}{x}$,解得x=4,
∴点C的坐标为(4,1.5).
如图,作AD⊥x轴于D,CE⊥x轴于E,则S△OAD=S△OCE,
∵S四边形OACE=S△OAC+S△OCE=S梯形ADEC+S△OAD,
∴S△OAC=S梯形ADEC=$\frac{1}{2}$(CE+AD)•DE=$\frac{1}{2}$(1.5+3)×2=4.5.
故答案为4.5.
点评 本题考查了反比例函数$y=\frac{k}{x}$中k的几何意义,待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,平行于x轴的直线上点的坐标特征,线段中点坐标公式,图形的面积等知识,难度适中.求出C点坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.圆有( )条对称轴.
| A. | 1 | B. | 2 | C. | 4 | D. | 无数条 |
12.下列式子一定是二次根式的是( )
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{x}$ | C. | $\sqrt{x+2}$ | D. | $\sqrt{{x^2}-2}$ |
9.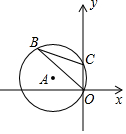 如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )
如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )
 如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )
如图,在平面直角坐标系中,半径为3的⊙A经过原点O和点C(0,2),若B是y轴左侧⊙A上一点,则sin∠OBC为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | 2$\sqrt{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2\sqrt{2}}{2}$ |
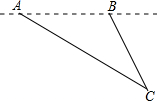 活动一:如图,飞机在距地面9km高空上飞行,先在A处测得正前方某小岛C的俯角为30°,飞行一段距离后,在B处测得该小岛的俯角为60°.求飞机的飞行距离.
活动一:如图,飞机在距地面9km高空上飞行,先在A处测得正前方某小岛C的俯角为30°,飞行一段距离后,在B处测得该小岛的俯角为60°.求飞机的飞行距离. 如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若点B离水平面的高度BC的长为30米,那么水管AB的长为60米.
如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若点B离水平面的高度BC的长为30米,那么水管AB的长为60米.