题目内容
 如图,直线l分别与⊙O1、⊙O2相切于点A、B,AO1=1,BO2=2.⊙O1沿着直线l的方向向右平移,当⊙O1与⊙O2相交时,AB长的范围为
如图,直线l分别与⊙O1、⊙O2相切于点A、B,AO1=1,BO2=2.⊙O1沿着直线l的方向向右平移,当⊙O1与⊙O2相交时,AB长的范围为考点:圆与圆的位置关系
专题:
分析:连接O1、O2,作 O1C⊥BO2于C,根据当两圆外切时,O1O2=1+2=3,然后利用O2C=2-1=1,结合勾股定理得到O1C=AB=
=2
,从而确定AB的取值范围.
| 32-12 |
| 2 |
解答:解:连接O1、O2 ,作 O1C⊥BO2于C,
,作 O1C⊥BO2于C,
当两圆外切时,O1O2=1+2=3,
∵O2C=2-1=1,
∴O1C=AB=
=2
,
∴0<AB<2
,
故答案为:0<AB<2
 ,作 O1C⊥BO2于C,
,作 O1C⊥BO2于C,当两圆外切时,O1O2=1+2=3,
∵O2C=2-1=1,
∴O1C=AB=
| 32-12 |
| 2 |
∴0<AB<2
| 2 |
故答案为:0<AB<2
| 2 |
点评:本题考查了圆与圆的位置关系,解题的关键是正确的构造直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=10,BD=8,AB=x,则x的取值范围是( )
| A、1<x<9 |
| B、2<x<18 |
| C、8<x<10 |
| D、4<x<5 |
 在矩形ABCD中,由9个边长均为1的正方形组成的“L型”模板如图放置,此时量得CF=3,则BC边的长度为
在矩形ABCD中,由9个边长均为1的正方形组成的“L型”模板如图放置,此时量得CF=3,则BC边的长度为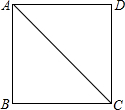 如图,在正方形ABCD中,对角线AC为2,则正方形边长为
如图,在正方形ABCD中,对角线AC为2,则正方形边长为