题目内容
在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=10,BD=8,AB=x,则x的取值范围是( )
| A、1<x<9 |
| B、2<x<18 |
| C、8<x<10 |
| D、4<x<5 |
考点:平行四边形的性质,三角形三边关系
专题:
分析:根据平行四边形的性质求出OA、OB,根据三角形的三边关系定理得到OA-OB<x<OA+OB,代入求出即可.
解答: 解:∵四边形ABCD是平行四边形,AC=10,BD=8,
解:∵四边形ABCD是平行四边形,AC=10,BD=8,
∴OA=OC=5,OD=OB=4,
在△OAB中,OA-OB<x<OA+OB,
∴5-4<x<4+5,
∴1<x<9.
故选:A.
 解:∵四边形ABCD是平行四边形,AC=10,BD=8,
解:∵四边形ABCD是平行四边形,AC=10,BD=8,∴OA=OC=5,OD=OB=4,
在△OAB中,OA-OB<x<OA+OB,
∴5-4<x<4+5,
∴1<x<9.
故选:A.
点评:本题考查了对平行四边形的性质,三角形的三边关系定理等知识点的理解和掌握,求出OA、OB后得出OA-OB<x<OA+OB是解此题的关键.

练习册系列答案
相关题目
分式方程
-1=
有增根,则m的值为( )
| x |
| x-1 |
| m |
| (x-1)(x+1) |
| A、0和2 | B、1 | C、1和-2 | D、2 |
若a>b,则下列不等式中,不成立的是( )
| A、a+5>b+5 |
| B、a-5>b-5 |
| C、5a>5b |
| D、-5a>-5b |
测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
| A、2.5m | B、2.25m |
| C、2m | D、3m |
 如图,直线l分别与⊙O1、⊙O2相切于点A、B,AO1=1,BO2=2.⊙O1沿着直线l的方向向右平移,当⊙O1与⊙O2相交时,AB长的范围为
如图,直线l分别与⊙O1、⊙O2相切于点A、B,AO1=1,BO2=2.⊙O1沿着直线l的方向向右平移,当⊙O1与⊙O2相交时,AB长的范围为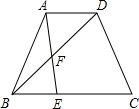 如图,等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,射线AB绕点A逆时针旋转分别与BD、BC交于点F、E,旋转角∠BAE=∠DBC,则BE=
如图,等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,射线AB绕点A逆时针旋转分别与BD、BC交于点F、E,旋转角∠BAE=∠DBC,则BE=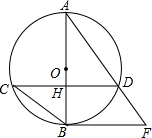 如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F.
如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F.