题目内容
19.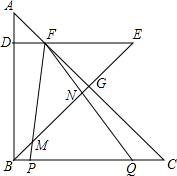 如图,△ABC是等腰直角三角形,点D在AB上,过D作DE⊥AB交AC于F,DE=BD,连接BE交AC于G.将一个45°角的顶点与点F重合,并绕点F旋转,这个角的两边分别交线段BC于P、Q两点,交BE于M、N两点.若AB=5,AD=1,CQ=1,则线段MN的长为$\frac{25\sqrt{2}}{14}$.
如图,△ABC是等腰直角三角形,点D在AB上,过D作DE⊥AB交AC于F,DE=BD,连接BE交AC于G.将一个45°角的顶点与点F重合,并绕点F旋转,这个角的两边分别交线段BC于P、Q两点,交BE于M、N两点.若AB=5,AD=1,CQ=1,则线段MN的长为$\frac{25\sqrt{2}}{14}$.
分析 如图,连接QE、MQ,作EH⊥FQ于H,作EH⊥FQ于H,先证明E、F、M、Q四点共圆,得MN•NE=FN•NQ,想办法求出EN、FN、NQ即可解决问题.
解答 解:如图,连接QE、MQ,作EH⊥FQ于H.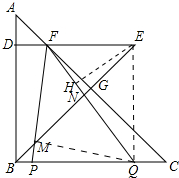
∵AB=BC,∠ABC=90°,AD=CQ=1,
∴BD=BQ=4,
∵DE⊥AB,
∴∠EDB=90°,
∴∠EDB+∠DBQ=180°,
∴DE∥BQ,BQ=BD=DE,
∴四边形DBQE是平行四边形,
∵∠DBQ=90°,
∴四边形DBQE是矩形,
∵DE=DB,
∴四边形DBQE是正方形,
∴∠BEQ=45°=∠MFQ,
∴E、F、M、Q四点共圆,
∴MN•NE=FN•NQ,
在RT△EFQ中,∵EF=3,EQ=4,
∴FQ=$\sqrt{E{F}^{2}+E{Q}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵EF∥BQ,
∴$\frac{EF}{BQ}$=$\frac{FN}{NQ}$=$\frac{3}{4}$
∴FN=$\frac{3}{7}$FQ=$\frac{15}{7}$,NQ=$\frac{4}{7}$FQ=$\frac{20}{7}$,作EH⊥FQ于H,
∵$\frac{1}{2}$•FQ•EH=$\frac{1}{2}$•EF•EQ,
∴EH=$\frac{12}{5}$,
∴FH=$\sqrt{E{F}^{2}-E{H}^{2}}$=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$,HN=FN-FH=$\frac{12}{35}$,
∴EN=$\sqrt{E{H}^{2}+H{N}^{2}}$=$\sqrt{(\frac{12}{5})^{2}+(\frac{12}{35})^{2}}$=$\frac{12\sqrt{2}}{7}$,
∴MN•$\frac{12\sqrt{2}}{7}$=$\frac{15}{7}$•$\frac{20}{7}$,
∴MN=$\frac{25\sqrt{2}}{14}$.
故答案为$\frac{25\sqrt{2}}{14}$.
点评 本题考查正方形的判定和性质、四点共圆、勾股定理等知识,解题的关键是利用相交弦定理,学会利用面积法求高,属于中考常考题型.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案 如图,在△ABC中,∠ACB=90°,CD⊥AB.垂足为D,E是AC的中点,ED、CB的延长线于点F.
如图,在△ABC中,∠ACB=90°,CD⊥AB.垂足为D,E是AC的中点,ED、CB的延长线于点F. 如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.
如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.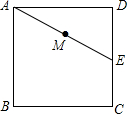 如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=$\frac{5}{2}$或$\frac{3}{2}$cm.
如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=$\frac{5}{2}$或$\frac{3}{2}$cm. 如图,在矩形纸片ABCD中,BC=40cm,AB=16cm,M点为BC边上的中点,点G沿B→A→D运动(不含端点),将矩形纸片沿直线MG翻折,使得点B落在AD边上,则折痕长度为10$\sqrt{5}$cm或8$\sqrt{5}$cm.
如图,在矩形纸片ABCD中,BC=40cm,AB=16cm,M点为BC边上的中点,点G沿B→A→D运动(不含端点),将矩形纸片沿直线MG翻折,使得点B落在AD边上,则折痕长度为10$\sqrt{5}$cm或8$\sqrt{5}$cm.