题目内容

7．一个三角形的两边长为3和6，若第三边取奇数，则此三角形的周长为14或16．

分析 根据三角形的三边关系可得6-3＜第三边＜6+3，求得第三边，再求三角形的周长即可．

解答 解：根据三角形的三边关系可得：6-3＜第三边＜6+3，
则3＜第三边＜9，
∵第三边取奇数，
∴第三边是5或7，
∴三角形的周长为14或16，
故答案为：14或16．

点评 此题主要考查了三角形的三边关系定理，关键是掌握三角形两边之和大于第三边；三角形的两边差小于第三边．

练习册系列答案
相关题目
4．如果圆锥底面圆的半径为3cm，它的侧面积为12πcm，那么它的母线长为4cm．
5．计算：
（1）$\frac{{a}^{2}}{a-3}$-a-3
（2）$\frac{3-m}{2m-4}$÷（m+2-$\frac{5}{m-2}$）
2．计算$\frac{{m}^{2}}{m-3}$-$\frac{9}{m-3}$的结果是（　　）
A．m+3B．m-3C．3-mD．-m-3
2．根据如图数轴表示，化简下式：|a+$\sqrt{2}$|-$\sqrt{（\sqrt{3}-b）^{2}}$-$\sqrt{（\sqrt{2}-b）^{2}}$．
12．计算：
（1）3$\sqrt{3}$-$\sqrt{8}$+$\sqrt{2}$-$\sqrt{27}$；
（2）（4$\sqrt{6}$-6$\sqrt{2}$）÷2$\sqrt{2}$；
（3）（2$\sqrt{5}$+5$\sqrt{2}$）（2$\sqrt{5}$-5$\sqrt{2}$）-（$\sqrt{5}$-$\sqrt{2}$）2
（4）7a$\sqrt{8a}$-4a2$\sqrt{\frac{1}{8a}}$+7a$\sqrt{2a}$．
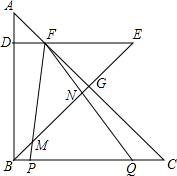19．如图，△ABC是等腰直角三角形，点D在AB上，过D作DE⊥AB交AC于F，DE=BD，连接BE交AC于G．将一个45°角的顶点与点F重合，并绕点F旋转，这个角的两边分别交线段BC于P、Q两点，交BE于M、N两点．若AB=5，AD=1，CQ=1，则线段MN的长为$\frac{25\sqrt{2}}{14}$．
16．如图，在△ABC中，AB＞AC，内切圆⊙I与边BC切于点D，AD与⊙I的另一个交点为E，⊙I的切线EP与BC的延长线交于点P，CF∥PE且与AD交于点F，直线BF与⊙I交于点M、N，M在线段BF上，线段PM与⊙I交于另一点Q．证明：∠ENP=∠ENQ．
17．已知点E（2，1）在二次函数y=x2-8x+m（m为常数）的图象上，则点E关于图象对称轴的对称点坐标是（　　）
A．（4，1）B．（5，1）C．（6，1）D．（7，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网