题目内容
13．
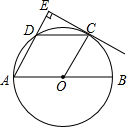如图，AB是⊙O的直径，点C、D为半圆O的三等分点，过点C作CE⊥AD，交AD的延长线于点E．求证：CE为⊙O的切线．
分析 由已知条件得出$\widehat{AD}=\widehat{CD}=\widehat{BC}$，由圆周角定理得出∠BOC=∠A，证出OC∥AD，再由已知条件得出CE⊥OC，即可证出CE为⊙O的切线．
解答 证明：∵点C、D为半圆O的三等分点，
∴$\widehat{AD}=\widehat{CD}=\widehat{BC}$，
∴∠BOC=∠A，
∴OC∥AD，
∵CE⊥AD，
∴CE⊥OC，
∴CE为⊙O的切线．
点评 本题考查了切线的判定、圆周角定理、平行线的判定；由圆周角定理证出OC∥AD是解决问题的关键．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于点E．若AC=6，BC=8，CD=3．