题目内容
1.计算:(1)$\frac{b}{a-b}+\frac{a}{a+b}-\frac{2ab}{{{b^2}-{a^2}}}$;
(2)$({\frac{1}{a-b}-\frac{b}{{{a^2}-{b^2}}}})÷\frac{a}{a+b}$.
分析 (1)原式通分并利用同分母分式的加减法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=$\frac{b(a+b)+a(a-b)+2ab}{(a+b)(a-b)}$=$\frac{(a+b)^{2}}{(a+b)(a-b)}$=$\frac{a+b}{a-b}$;
(2)原式=$\frac{a+b-b}{(a+b)(a-b)}$•$\frac{a+b}{a}$=$\frac{a}{(a+b)(a-b)}$•$\frac{a+b}{a}$=$\frac{1}{a-b}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.下列二次根式中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{18}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{\frac{3}{2}}$ |
6.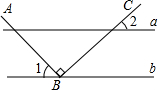 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 125° |
10.一个直角三角形中,两条直角边长为3和4,则它的斜边长为( )
| A. | 2 | B. | $\sqrt{7}$ | C. | 5 | D. | 25 |
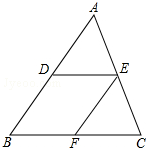 如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.试问当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.试问当△ABC满足什么条件时,四边形DBFE是菱形?为什么?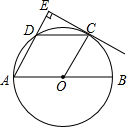 如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.求证:CE为⊙O的切线.
如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.求证:CE为⊙O的切线.