题目内容
11.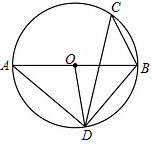 如图,AB是⊙O的直径,C,D两点在⊙O上,若∠C=40°
如图,AB是⊙O的直径,C,D两点在⊙O上,若∠C=40°①求∠ABD的度数;
②已知OA=2,求BD的长.(sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果精确到0.1)
分析 ①根据圆周角定理得到∠ADB=90°,∠A=∠C=40°,然后利用互余计算∠ABD;
②在Rt△ABD中利用正弦的定义计算BD的长.
解答 解:①∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠A=∠C=40°,
∴∠ABD=90°-∠A=50°;
②在Rt△ABD中,AB=2OA=4,
∵sinA=$\frac{BD}{AB}$,
∴BD=4sin40°=4×0.64≈2.6.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
1.下列运算中,正确的是( )
| A. | $\sqrt{2}$+2$\sqrt{3}$=3$\sqrt{5}$ | B. | 15x3-7x3=8x3 | C. | (-xy)2=-x2y2 | D. | x6÷x2=x3 |
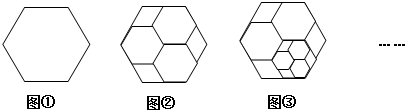
 如图,小宇用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第10个图案中共有121个黑子.
如图,小宇用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第10个图案中共有121个黑子.