题目内容
16.观察下列关于自然数的等式:32-4×1=4+1 ①
52-4×2=16+1 ②
72-4×3=36+1 ③
…
根据上述规律解决下列问题:
(1)完成第四个等式:92-4×4=64+1;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
分析 (1)第一个数是奇数,第二个数是序号数,第三个数是第一个数减1的平方,由此即可写出结果.
(2)第一个数用(2n+1)2表示,接下来不难写出等式,根据恒等式的证明方法进行证明即可.
解答 解:(1)第四个等式:92-4×4=64+1
故答案分别为9,4,64.
(2)(2n+1)2-4n=(2n)2+1,
验证:左边=(2n+1)2-4×n=4n2+4n+1-4n=4n2+1
左边=右边,
所以结论成立.
点评 本题考查规律型:数字的变化类问题,解题的关键是学会从一般到特殊的探究方法,找到规律后即可解决问题属于中考常考题型.

练习册系列答案
相关题目
4.图中是正方体的展开图的共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.在x=-4,0,-1.2,π中满足不等式组$\left\{\begin{array}{l}{x<2}\\{2(x+1)>-2}\end{array}\right.$的x值是( )
| A. | -4和0 | B. | -4和-1.2 | C. | 0和π | D. | -1.2和0 |
 如图,在Rt△ABC中,∠B=60°,BC=3,D为BC边上的三等分点,BD=2CD,E为AB边上一动点,将△DBE沿DE折叠到△DB′E的位置,连接AB′,则线段AB′的最小值为:2$\sqrt{7}$-2.
如图,在Rt△ABC中,∠B=60°,BC=3,D为BC边上的三等分点,BD=2CD,E为AB边上一动点,将△DBE沿DE折叠到△DB′E的位置,连接AB′,则线段AB′的最小值为:2$\sqrt{7}$-2.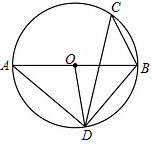 如图,AB是⊙O的直径,C,D两点在⊙O上,若∠C=40°
如图,AB是⊙O的直径,C,D两点在⊙O上,若∠C=40°