题目内容
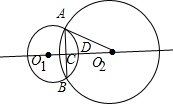 如图,⊙O1与⊙O2相交于A、B两点,O2A切⊙O1于点A,O1O2与AB交于点C,与⊙O1交于点D.若AB=8,CD=2,则tan∠AO2C=
如图,⊙O1与⊙O2相交于A、B两点,O2A切⊙O1于点A,O1O2与AB交于点C,与⊙O1交于点D.若AB=8,CD=2,则tan∠AO2C=考点:相交两圆的性质
专题:
分析:如图,作辅助线;证明O1O2⊥AB,AC=BC=4;O1A⊥AO2;根据射影定理列出关于λ、μ的方程组,求出λ、μ即可解决问题.
解答: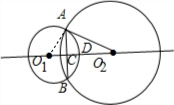 解:如图,连接O1A;
解:如图,连接O1A;
∵⊙O1与⊙O2相交于A、B两点,且O2A切⊙O1于点A,
∴O1O2⊥AB,AC=BC=4;O1A⊥AO2;
设⊙O1的半径为λ,则O1C=λ-2;设O2C=μ;
由射影定理得:
,
解得:λ=5,μ=
,
∴tan∠AO2C=
=
,
故答案为
.
 解:如图,连接O1A;
解:如图,连接O1A;∵⊙O1与⊙O2相交于A、B两点,且O2A切⊙O1于点A,
∴O1O2⊥AB,AC=BC=4;O1A⊥AO2;
设⊙O1的半径为λ,则O1C=λ-2;设O2C=μ;
由射影定理得:
|
解得:λ=5,μ=
| 16 |
| 3 |
∴tan∠AO2C=
| AC |
| O2C |
| 3 |
| 4 |
故答案为
| 3 |
| 4 |
点评:该题以圆为载体,主要考查了相交两圆的性质、射影定理、正切三角函数的定义等几何知识点及其应用问题;深入观察图形,数形结合,准确找出图形中隐含的数量关系是解题的关键.

练习册系列答案
相关题目
下列命题的逆命题是真命题的是( )
| A、如果两个角不相等,那么这两个角不是对顶角 |
| B、如果a=b,那么a2=b2 |
| C、如果两个角相等,那么这两个角是同位角 |
| D、如果一个整数能被5整除,则这个整数的个位数字是0 |
下列关于三角形全等的判定,其中正确的是( )
| A、有两边和第三边上的中线对应相等的两个三角形全等 |
| B、有两边和其中一边上的高对应相等的两个三角形全等 |
| C、有两边和第三边上的高对应相等的两个三角形全等 |
| D、三边中,有两边对应相等的两个三角形全等 |
下面计算正确的是( )
| A、a+a2=a3 |
| B、(a-b)2=a2-b2 |
| C、a6÷a3=a2 |
| D、(-a)3•a2=-a5 |
 小华和小苗练习射击,两人的成绩如图所示,小华和小苗两人成绩的方差分别为
小华和小苗练习射击,两人的成绩如图所示,小华和小苗两人成绩的方差分别为
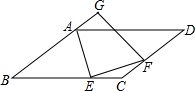 如图,?ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF,若BC=7,DF=3,tan∠AEB=3,则GF的长为
如图,?ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF,若BC=7,DF=3,tan∠AEB=3,则GF的长为