题目内容
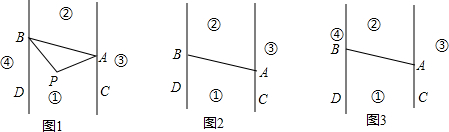
如图,直线AC∥BD,连接AB.直线AC,直线BD,线段AB把平面分成①,②,③,④四个部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角(规定:线上各点不属于任何部分;有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?若成立,请证明,若不成立,请直接写出三个角之间的关系.
(3)当动点P落在第③部分时,全面探究三角之间的关系,并证明.
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?若成立,请证明,若不成立,请直接写出三个角之间的关系.
(3)当动点P落在第③部分时,全面探究三角之间的关系,并证明.

考点:平行线的性质
专题:
分析:(1)如图1,延长BP交直线AC于点E,由AC∥BD,可知∠PEA=∠PBD.由∠APB=∠PAE+∠PEA,可知∠APB=∠PAC+∠PBD;
(2)过点P作AC的平行线,根据平行线的性质解答;
(3)根据P的不同位置,分三种情况讨论.
(2)过点P作AC的平行线,根据平行线的性质解答;
(3)根据P的不同位置,分三种情况讨论.
解答:解:(1)解法一:如图1延长BP交直线AC于点E.
∵AC∥BD,
∴∠PEA=∠PBD.
∵∠APB=∠PAE+∠PEA,
∴∠APB=∠PAC+∠PBD;


解法二:如图2
过点P作FP∥AC,
∴∠PAC=∠APF.
∵AC∥BD,
∴FP∥BD.
∴∠FPB=∠PBD.
∴∠APB=∠APF+∠FPB=∠PAC+∠PBD;
解法三:如图3,
∵AC∥BD,
∴∠CAB+∠ABD=180°,
∠PAC+∠PAB+∠PBA+∠PBD=180°.
又∵∠APB+∠PBA+∠PAB=180°,
∴∠APB=∠PAC+∠PBD.
(2)不成立.
(3)(a)当动点P在射线BA的右侧时,如图3,结论是
∠PBD=∠PAC+∠APB.
(b)当动点P在射线BA上,如图4,
结论是∠PBD=∠PAC+∠APB.
或∠PAC=∠PBD+∠APB或∠APB=0°,
∠PAC=∠PBD(任写一个即可).
(c)当动点P在射线BA的左侧时,如图5
结论是∠PAC=∠APB+∠PBD.
选择(a)证明:
如图3,连接PA,连接PB交AC于M.
∵AC∥BD,
∴∠PMC=∠PBD.
又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠PBD=∠PAC+∠APB.
选择(b)证明:如图4
∵点P在射线BA上,∴∠APB=0度.
∵AC∥BD,∴∠PBD=∠PAC.
∴∠PBD=∠PAC+∠APB
或∠PAC=∠PBD+∠APB
或∠APB=0°,∠PAC=∠PBD.
选择(c)证明:
如图5,连接PA,连接PB交AC于F
∵AC∥BD,
∴∠PFA=∠PBD.
∵∠PAC=∠APF+∠PFA,
∴∠PAC=∠APB+∠PBD.
∵AC∥BD,
∴∠PEA=∠PBD.
∵∠APB=∠PAE+∠PEA,
∴∠APB=∠PAC+∠PBD;


解法二:如图2
过点P作FP∥AC,
∴∠PAC=∠APF.
∵AC∥BD,
∴FP∥BD.
∴∠FPB=∠PBD.
∴∠APB=∠APF+∠FPB=∠PAC+∠PBD;
解法三:如图3,
∵AC∥BD,
∴∠CAB+∠ABD=180°,
∠PAC+∠PAB+∠PBA+∠PBD=180°.
又∵∠APB+∠PBA+∠PAB=180°,
∴∠APB=∠PAC+∠PBD.
(2)不成立.
(3)(a)当动点P在射线BA的右侧时,如图3,结论是

∠PBD=∠PAC+∠APB.
(b)当动点P在射线BA上,如图4,
结论是∠PBD=∠PAC+∠APB.
或∠PAC=∠PBD+∠APB或∠APB=0°,
∠PAC=∠PBD(任写一个即可).
(c)当动点P在射线BA的左侧时,如图5
结论是∠PAC=∠APB+∠PBD.
选择(a)证明:
如图3,连接PA,连接PB交AC于M.
∵AC∥BD,
∴∠PMC=∠PBD.
又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠PBD=∠PAC+∠APB.
选择(b)证明:如图4
∵点P在射线BA上,∴∠APB=0度.
∵AC∥BD,∴∠PBD=∠PAC.
∴∠PBD=∠PAC+∠APB
或∠PAC=∠PBD+∠APB
或∠APB=0°,∠PAC=∠PBD.
选择(c)证明:
如图5,连接PA,连接PB交AC于F
∵AC∥BD,
∴∠PFA=∠PBD.
∵∠PAC=∠APF+∠PFA,
∴∠PAC=∠APB+∠PBD.
点评:此题考查了角平分线的性质;是一道探索性问题,旨在考查同学们对材料的分析研究能力和对平行线及角平分线性质的掌握情况.认真做好(1)(2)小题,可以为(3)小题提供思路.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
二次函数y=(x-
)(mx-4m)(其中m>0),下列说法正确的( )
| 1 |
| m |
| A、当x>2时,都有y随着x的增大而增大 | ||
| B、当x<3时,都有y随着x的增大而减小 | ||
C、若当x<n时,都有y随着x的增大而减小,则n≤2+
| ||
D、若当x<n时,都有y随着x的增大而减小,则n≥
|
直角三角形的边各扩大(或缩小)相同的倍数,此三角形( )
| A、仍为直角三角形 |
| B、可能是锐角三角形 |
| C、可能是钝角三角形 |
| D、不可能是直角三角形 |
某城市自来水收费实行阶梯水价,收费标准如下表所示:
若某用户4月份交水费25元,则4月份所用水量是( )
| 月用水量 | 不超过10m3的部分 | 超过10m3不超过16m3的部分 |
| 收费标准(元/m3) | 2.00 | 2.50 |
| A、10m3 |
| B、12m3 |
| C、14m3 |
| D、16m3 |
若ab>0,bc<0,则y=-
x+
经过( )
| a |
| b |
| a |
| c |
| A、第一、二、三象限 |
| B、第二、三、四象限 |
| C、第一、二、四象限 |
| D、第一、三、四象限 |
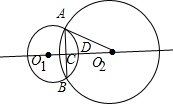 如图,⊙O1与⊙O2相交于A、B两点,O2A切⊙O1于点A,O1O2与AB交于点C,与⊙O1交于点D.若AB=8,CD=2,则tan∠AO2C=
如图,⊙O1与⊙O2相交于A、B两点,O2A切⊙O1于点A,O1O2与AB交于点C,与⊙O1交于点D.若AB=8,CD=2,则tan∠AO2C= 根据题意可知,下列判断中所依据的命题或定理是
根据题意可知,下列判断中所依据的命题或定理是