题目内容
下列关于三角形全等的判定,其中正确的是( )
| A、有两边和第三边上的中线对应相等的两个三角形全等 |
| B、有两边和其中一边上的高对应相等的两个三角形全等 |
| C、有两边和第三边上的高对应相等的两个三角形全等 |
| D、三边中,有两边对应相等的两个三角形全等 |
考点:全等三角形的判定
专题:
分析:根据全等三角形的判定定理,根据各选项的表述,分别判定是否满足几种判定定理的一种,从而可得出答案.
解答:解:A、有两边和第三边上的中线对应相等的两个三角形全等,故本选项正确;
B、如图,ABCD是平行四边形,在△ABC与△DBC中,BC=BC,AB=DC,BC边上的高相等,显然△ABC与△DBC不全等,故本选项错误;

C、如图,△ABC与△ABC′中,AB=AB,AC=AC′,高AD相同,但是,△ABC与△ABC′不全等,故本选项错误;

D、三边中,有两边对应相等,但是夹角不相等时两个三角形不全等,故本选项错误.
故选A.
B、如图,ABCD是平行四边形,在△ABC与△DBC中,BC=BC,AB=DC,BC边上的高相等,显然△ABC与△DBC不全等,故本选项错误;

C、如图,△ABC与△ABC′中,AB=AB,AC=AC′,高AD相同,但是,△ABC与△ABC′不全等,故本选项错误;

D、三边中,有两边对应相等,但是夹角不相等时两个三角形不全等,故本选项错误.
故选A.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为( )
| A、3 | B、13 |
| C、3或5 | D、3或13 |
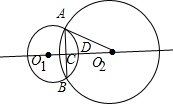 如图,⊙O1与⊙O2相交于A、B两点,O2A切⊙O1于点A,O1O2与AB交于点C,与⊙O1交于点D.若AB=8,CD=2,则tan∠AO2C=
如图,⊙O1与⊙O2相交于A、B两点,O2A切⊙O1于点A,O1O2与AB交于点C,与⊙O1交于点D.若AB=8,CD=2,则tan∠AO2C= 根据题意可知,下列判断中所依据的命题或定理是
根据题意可知,下列判断中所依据的命题或定理是