题目内容
课后,数学兴趣小组继续探究:
(1)当∠B是直角时,如图1,在△ABC和△DEF中,AB=DE,AC=DF,∠B=∠E=90°,求证:△ABC≌△DEF.
(2)当∠B是钝角时,如图2,在△ABC和△DEF中,AB=DE,AC=DF,∠B=∠E,且∠B、∠E都是钝角,此时△ABC与△DEF会全等吗?请说明理由.
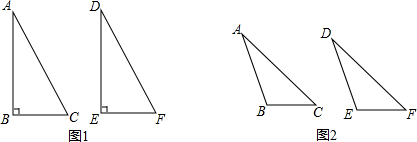
(1)当∠B是直角时,如图1,在△ABC和△DEF中,AB=DE,AC=DF,∠B=∠E=90°,求证:△ABC≌△DEF.
(2)当∠B是钝角时,如图2,在△ABC和△DEF中,AB=DE,AC=DF,∠B=∠E,且∠B、∠E都是钝角,此时△ABC与△DEF会全等吗?请说明理由.
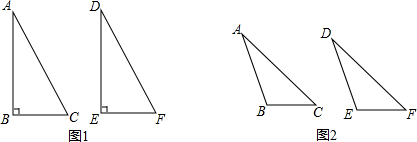
考点:全等三角形的判定
专题:
分析:(1)由全等三角形的判定定理HL证得结论;
(2)若已知两边对应相等,则找它们的夹角或第三边对应相等.
(2)若已知两边对应相等,则找它们的夹角或第三边对应相等.
解答:(1)证明:∵∠B=∠E=90°,
∴在Rt△ABC与Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL);
(2)△ABC与△DEF不一定全等.理由如下:
∵AB=DE,AC=DF,
∴∠B、不是AB与AC的夹角,∠E不是DE与DF的夹角,
∴△ABC与△DEF不一定全等.
∴在Rt△ABC与Rt△DEF中,
|
∴Rt△ABC≌Rt△DEF(HL);
(2)△ABC与△DEF不一定全等.理由如下:
∵AB=DE,AC=DF,
∴∠B、不是AB与AC的夹角,∠E不是DE与DF的夹角,
∴△ABC与△DEF不一定全等.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
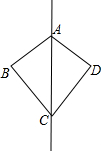
 如图,△ABC的顶点A、B、C均在⊙O上,AB=AC,∠AOC=60°,则∠ACB的大小是( )
如图,△ABC的顶点A、B、C均在⊙O上,AB=AC,∠AOC=60°,则∠ACB的大小是( )| A、30° | B、45° |
| C、60° | D、70° |
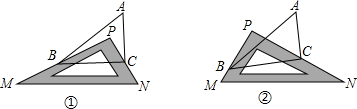
 如图,△ABC与△ADC关于AC所在的直线对称,∠BCD=70°,∠B=80°,则∠DAC的度数为( )
如图,△ABC与△ADC关于AC所在的直线对称,∠BCD=70°,∠B=80°,则∠DAC的度数为( )| A、55° | B、65° |
| C、75° | D、85° |
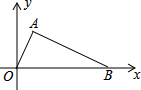 如图,已知A(1,2),B(5,0),O(0,0),试判断△ABO的形状,并说明理由.
如图,已知A(1,2),B(5,0),O(0,0),试判断△ABO的形状,并说明理由.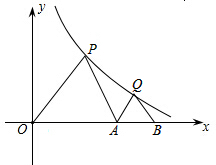 △POA、△QAB都是等边三角形,点P、Q都在双曲线y=
△POA、△QAB都是等边三角形,点P、Q都在双曲线y=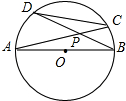 如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.
如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.