题目内容
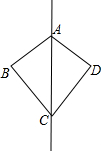 如图,△ABC与△ADC关于AC所在的直线对称,∠BCD=70°,∠B=80°,则∠DAC的度数为( )
如图,△ABC与△ADC关于AC所在的直线对称,∠BCD=70°,∠B=80°,则∠DAC的度数为( )| A、55° | B、65° |
| C、75° | D、85° |
考点:轴对称的性质
专题:
分析:根据轴对称的性质:对应角相等,可得∠D,∠ACD的度数,根据三角形的内角和定理,可得答案.
解答:解:由△ABC与△ADC关于AC所在的直线对称,∠BCD=70°,∠B=80°,得
∠D=∠B=80°,∠ACD=∠ACB=
∠BCD=
×70°=35°.
由三角形内角和定理,得
∠DAC=180°-∠D-∠ACD=180°-80°-35°=65°,
故选:B.
∠D=∠B=80°,∠ACD=∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
由三角形内角和定理,得
∠DAC=180°-∠D-∠ACD=180°-80°-35°=65°,
故选:B.
点评:本题考查了轴对称的性质,利用了轴对称的性质,三角形的内角和定理.

练习册系列答案
相关题目
 如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙的长为18米,在与墙垂直的一边要开一扇2米宽的门,已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库的宽和长分别为多少米?
如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙的长为18米,在与墙垂直的一边要开一扇2米宽的门,已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库的宽和长分别为多少米?长城总长约为6 700 000米,用科学记数法表示正确的是( )
| A、6.7×108米 |
| B、6.7×107米 |
| C、6.7×106米 |
| D、6.7×105米 |
 如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,成为第一次操作;然后,将其中一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2014个小正方形,则需要操作的次数是( )
如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,成为第一次操作;然后,将其中一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2014个小正方形,则需要操作的次数是( )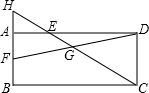 如图,在矩形ABCD中,E、F分别是AD、AB边上的点,连接CE、DF,他们相交于点G,延长CE交BA的延长线于点H,则图中的相似三角形共有( )
如图,在矩形ABCD中,E、F分别是AD、AB边上的点,连接CE、DF,他们相交于点G,延长CE交BA的延长线于点H,则图中的相似三角形共有( )