题目内容
如图①,在△ABC中,∠A=50°,有一块直角三角尺PMN放置在△ABC上(点P在△ABC内),使三角尺PMN的两条直角边PM、PN恰好分别经过点B、C.
(1)填空:∠ABC+∠ACB= ,∠PBC+∠PCB= ;
(2)试问∠ABP与∠ACP是否存在某种确定的数量关系,请写出你的结论;
(3)如图②,改变直角三角尺PMN的位置(点P在△ABC外),三角尺PMN的两条直角边PM、PN仍然分别经过点B、C,(2)中的结论是否仍然成立?若不成立,请写出你的结论,并说明理由.
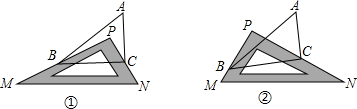
(1)填空:∠ABC+∠ACB=
(2)试问∠ABP与∠ACP是否存在某种确定的数量关系,请写出你的结论;
(3)如图②,改变直角三角尺PMN的位置(点P在△ABC外),三角尺PMN的两条直角边PM、PN仍然分别经过点B、C,(2)中的结论是否仍然成立?若不成立,请写出你的结论,并说明理由.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)已知∠A=50°,根据三角形内角和定理易求∠ABC+∠ACB的度数.已知∠P=90°,根据三角形内角和定理易求∠PBC+∠PCB的度数;
(2)由(1)中∠ABC+∠ACB的度数,∠PBC+∠PCB的度数,相减即可得到∠ABP与∠ACP之间的数量关系;
(3)发生变化,由于在△ABC中,∠A=50°,从而∠ABC+∠ACB是一个定值,即等于140°,同理在△PBC中,∠BPC=90°,那么∠PBC+∠PCB=90°,于是∠ACP-∠ABP=130°-90°=40°.
(2)由(1)中∠ABC+∠ACB的度数,∠PBC+∠PCB的度数,相减即可得到∠ABP与∠ACP之间的数量关系;
(3)发生变化,由于在△ABC中,∠A=50°,从而∠ABC+∠ACB是一个定值,即等于140°,同理在△PBC中,∠BPC=90°,那么∠PBC+∠PCB=90°,于是∠ACP-∠ABP=130°-90°=40°.
解答:解:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABC+∠ACB=130°;∠PBC+∠PCB=90°.
(2)∠ABP+∠ACP=40°.
∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABP+∠ACP
=(∠ABC-∠PBC)+(∠ACB-∠PCB)
=(∠ABC+∠ACB)-(∠PBC+∠PCB)
=130°-90°
=40°.
(3)发生变化.
∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,(三角形内角和180°)
∵∠MPN=90°,
∴∠PBC+∠PCB=90°,(三角形内角和180°)
∴∠ACP-∠ABP=130°-90°=40°.
∴∠ABC+∠ACB=180°-50°=130°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABC+∠ACB=130°;∠PBC+∠PCB=90°.
(2)∠ABP+∠ACP=40°.
∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABP+∠ACP
=(∠ABC-∠PBC)+(∠ACB-∠PCB)
=(∠ABC+∠ACB)-(∠PBC+∠PCB)
=130°-90°
=40°.
(3)发生变化.
∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,(三角形内角和180°)
∵∠MPN=90°,
∴∠PBC+∠PCB=90°,(三角形内角和180°)
∴∠ACP-∠ABP=130°-90°=40°.
点评:本题考查的是三角形内角和定理:三角形三个内角的和等于180°.注意运用整体法计算.关键是求出∠ABC+∠ACB,∠PBC+∠PCB的度数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
长城总长约为6 700 000米,用科学记数法表示正确的是( )
| A、6.7×108米 |
| B、6.7×107米 |
| C、6.7×106米 |
| D、6.7×105米 |
已知一矩形的两边长分别为7cm和12cm,其中一个内角的平分线分长边为两部分,这两部分的长分别为( )
| A、6cm和6cm |
| B、7cm和5cm |
| C、4cm和8cm |
| D、3cm和9cm |
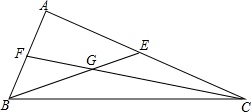 如图,△ABC的中线BE、CF相交于G,且AB=12,AC=16,BC=20,求GC的长.
如图,△ABC的中线BE、CF相交于G,且AB=12,AC=16,BC=20,求GC的长.
 如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,成为第一次操作;然后,将其中一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2014个小正方形,则需要操作的次数是( )
如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,成为第一次操作;然后,将其中一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2014个小正方形,则需要操作的次数是( )