题目内容
6.计算(1)-16-(-12)-(+8)
(2)(-1$\frac{1}{3}$)×(+$\frac{3}{4}$)×(-$\frac{2}{3}$)
(3)-5×(-$1\frac{4}{5}$)-(+9)×(-$1\frac{1}{3}$)
(4)(-15)×(-9$\frac{13}{15}$)
分析 (1)(2)从左向右依次计算,求出算式的值是多少即可.
(3)首先计算乘法,然后计算减法即可.
(4)首先把-9$\frac{13}{15}$分成-10+$\frac{2}{15}$,然后根据乘法分配律计算即可.
解答 解:(1)-16-(-12)-(+8)
=-4-8
=-12
(2)(-1$\frac{1}{3}$)×(+$\frac{3}{4}$)×(-$\frac{2}{3}$)
=(-1)×(-$\frac{2}{3}$)
=$\frac{2}{3}$
(3)-5×(-$1\frac{4}{5}$)-(+9)×(-$1\frac{1}{3}$)
=9-(-12)
=9+12
=21
(4)(-15)×(-9$\frac{13}{15}$)
=(-15)×(-10+$\frac{2}{15}$)
=(-15)×(-10)+(-15)×$\frac{2}{15}$
=150-2
=148
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,注意乘法分配律的应用.

练习册系列答案
相关题目
16. 如图,矩形ABCD中,AC,BD相交于点O,若∠AOB=60°,AC=6,则AB的长为( )
如图,矩形ABCD中,AC,BD相交于点O,若∠AOB=60°,AC=6,则AB的长为( )
 如图,矩形ABCD中,AC,BD相交于点O,若∠AOB=60°,AC=6,则AB的长为( )
如图,矩形ABCD中,AC,BD相交于点O,若∠AOB=60°,AC=6,则AB的长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | $3\sqrt{3}$ | D. | 6 |
16.在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
(1)表中a的值等于0.25;
(2)估算口袋中白球的个数;
(3)用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 |
| 摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
| 摸到黑球的频率 $\frac{m}{n}$ | 0.26 | 0.247 | 0.245 | 0.248 | a |
(2)估算口袋中白球的个数;
(3)用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
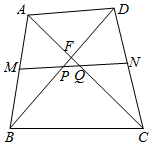 如图,四边形ABCD的对角线AC,BD相交于点F,M,N分别为AB,CD的中点,连接MN分别交BD,AC于点P,Q,且∠FPQ=∠FQP,若BD=9,则AC=9.
如图,四边形ABCD的对角线AC,BD相交于点F,M,N分别为AB,CD的中点,连接MN分别交BD,AC于点P,Q,且∠FPQ=∠FQP,若BD=9,则AC=9.
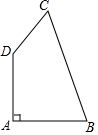 如图,在四边形ABCD中,DA⊥AB,DA=AB=$\sqrt{2}$,BC=$\sqrt{5}$,DC=1.则∠ADC的度数是135°.
如图,在四边形ABCD中,DA⊥AB,DA=AB=$\sqrt{2}$,BC=$\sqrt{5}$,DC=1.则∠ADC的度数是135°. 篮球场上,小金、小木、小火、小水、小土五人打算先选出一人做裁判,然后将其余四人组成两队打比赛,选人规则如下:五人都伸出右脚,让五个脚尖围在一起成“圆圈”状,其中一人将球从“圆圈”的中心处向上竖直抛起,球落到地面上弹起、落下如此反复,直到停止运动,在此过程中,篮球碰到谁的脚尖,谁就将脚收回,直到剩下两人时,选人结束,第一个收回脚的是裁判,第二、三个收回脚的为一队,剩下的两人为另一队,若截止到球停止运动时碰到的脚尖小于三个,则重新考试.前按此规则,思考下面问题并回答:
篮球场上,小金、小木、小火、小水、小土五人打算先选出一人做裁判,然后将其余四人组成两队打比赛,选人规则如下:五人都伸出右脚,让五个脚尖围在一起成“圆圈”状,其中一人将球从“圆圈”的中心处向上竖直抛起,球落到地面上弹起、落下如此反复,直到停止运动,在此过程中,篮球碰到谁的脚尖,谁就将脚收回,直到剩下两人时,选人结束,第一个收回脚的是裁判,第二、三个收回脚的为一队,剩下的两人为另一队,若截止到球停止运动时碰到的脚尖小于三个,则重新考试.前按此规则,思考下面问题并回答: