题目内容
梯形两条对角线长分别是6、8且互相垂直,则该梯形的中位线长为 .
考点:梯形中位线定理,勾股定理
专题:
分析:过D作DE∥AC交BC的延长线于E,得出平行四边形ACED,得出AD=CE,AC∥DE,AC=DE=8,求出∠BDE=90°,根据勾股定理求出BE,根据梯形的中位线求出即可.
解答:解: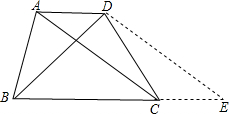
过D作DE∥AC交BC的延长线于E,
∵AD∥BC,ED∥AC,
∴四边形ACED是平行四边形,
∴AD=CE,AC∥DE,AC=DE=8,
∵AC⊥BD,
∴BD⊥DE,
即∠BDE=90°,
∵在Rt△BDE中,BD=6,DE=8,由勾股定理得:BE=10,
即BC+AD=10,
∴梯形ABCD的中位线长是
(BC+AD)=5,
故答案为5.

过D作DE∥AC交BC的延长线于E,
∵AD∥BC,ED∥AC,
∴四边形ACED是平行四边形,
∴AD=CE,AC∥DE,AC=DE=8,
∵AC⊥BD,
∴BD⊥DE,
即∠BDE=90°,
∵在Rt△BDE中,BD=6,DE=8,由勾股定理得:BE=10,
即BC+AD=10,
∴梯形ABCD的中位线长是
| 1 |
| 2 |
故答案为5.
点评:本题考查了梯形的中位线、平行四边形的性质和判定、勾股定理得应用,关键是把梯形转化成平行四边形和三角形.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
如果三角形内有一点到三边距离相等,且到三顶点的距离也相等,那么这个三角形的形状是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
已知a、b为实数且ab=1,设P=
+
,Q=
+
;则P、Q的大小关系为( )
| 1 |
| a+1 |
| 1 |
| b+1 |
| a |
| a+1 |
| b |
| b+1 |
| A、P>Q | B、P<Q |
| C、P=Q | D、大小关系不能确定 |
若(a+b)2=49,ab=6,则a-b的值为( )
| A、-5 | B、±5 | C、5 | D、±4 |
下列各式计算正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,正方形ABCD的边长为8厘米,E,F,G,H分别是AD,EC,FB,GA的中点,CE与DH的交点为I,求四边形FGHI的面积.
如图,正方形ABCD的边长为8厘米,E,F,G,H分别是AD,EC,FB,GA的中点,CE与DH的交点为I,求四边形FGHI的面积. 如图,分别以边长2为的等边三角形ABC的顶点为圆心,以其边长为半径作三个等圆,得交点D、E、F,连接CF交⊙C于点G,以点E为圆心,EG长为半径画弧,交边AB于点M,交边BC于点N,连接MN,求MN的长.
如图,分别以边长2为的等边三角形ABC的顶点为圆心,以其边长为半径作三个等圆,得交点D、E、F,连接CF交⊙C于点G,以点E为圆心,EG长为半径画弧,交边AB于点M,交边BC于点N,连接MN,求MN的长.