题目内容
 如图,分别以边长2为的等边三角形ABC的顶点为圆心,以其边长为半径作三个等圆,得交点D、E、F,连接CF交⊙C于点G,以点E为圆心,EG长为半径画弧,交边AB于点M,交边BC于点N,连接MN,求MN的长.
如图,分别以边长2为的等边三角形ABC的顶点为圆心,以其边长为半径作三个等圆,得交点D、E、F,连接CF交⊙C于点G,以点E为圆心,EG长为半径画弧,交边AB于点M,交边BC于点N,连接MN,求MN的长.考点:圆的综合题
专题:压轴题
分析:如图,过点E作EP⊥AB,连接EA、EC,易得△EAC为正三角形,△ABC为正三角形;由正三角形的性质、平行线的性质求得△ECG为等腰直角三角形,根据勾股定理、圆的半径的性质推知EM=EG=2
;
然后在直角△EPA和直角△EPM中由勾股定理、线段间的和差关系求得AM、BM的长度;最后根据M,N关于BE对称的特点以及平行线的判定可以证得△BMN为等边三角形,从而得知NM=3-
.
| 2 |
然后在直角△EPA和直角△EPM中由勾股定理、线段间的和差关系求得AM、BM的长度;最后根据M,N关于BE对称的特点以及平行线的判定可以证得△BMN为等边三角形,从而得知NM=3-
| 5 |
解答: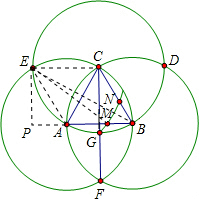 解:如图,过点E作EP⊥AB,连接EA、EC、EM.
解:如图,过点E作EP⊥AB,连接EA、EC、EM.
∵在⊙C中,EC=AC;在⊙A中,AE=AC,
∴EC=AC=AE,
∴△EAC为正三角形;
同理证得△ABC为正三角形,则∠ECA=∠CAB=60°,
∴EC∥AB,
又∵由相交两圆的性质得:CG⊥AB,
∴EC⊥CG,
∴EM=EG=
=2
,
∵∠EAP=60°,
∴EP=
,AP=1,PM=
=
,
∴AM=PM-AP=
-1,
∴BM=AB-AM=2-(
-1)=3-
;
又由对称性可知M,N关于BE对称,BN=BM=3-
且MN∥AC,
∴△BMN为等边三角形,即NM=3-
.
 解:如图,过点E作EP⊥AB,连接EA、EC、EM.
解:如图,过点E作EP⊥AB,连接EA、EC、EM.∵在⊙C中,EC=AC;在⊙A中,AE=AC,
∴EC=AC=AE,
∴△EAC为正三角形;
同理证得△ABC为正三角形,则∠ECA=∠CAB=60°,
∴EC∥AB,
又∵由相交两圆的性质得:CG⊥AB,
∴EC⊥CG,
∴EM=EG=
| 22+22 |
| 2 |
∵∠EAP=60°,
∴EP=
| 3 |
| EM2-EP2 |
| 5 |
∴AM=PM-AP=
| 5 |
∴BM=AB-AM=2-(
| 5 |
| 5 |
又由对称性可知M,N关于BE对称,BN=BM=3-
| 5 |
∴△BMN为等边三角形,即NM=3-
| 5 |
点评:本题考查了圆的综合题.此题涉及到的知识点有:勾股定理、等边三角形的判定与性质以及线段间的和差关系.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,△ABC中AB=AC,AB的垂直平分线交BC于E,EC的垂直平分线交DE延长线于M,若∠FMD=40°,则∠BAC等于( )
如图,△ABC中AB=AC,AB的垂直平分线交BC于E,EC的垂直平分线交DE延长线于M,若∠FMD=40°,则∠BAC等于( )| A、120° | B、110° |
| C、100° | D、90° |
 如图,已知AB∥CD,AE=CF,则下列条件中不一定能使△ABE≌△CDF的是( )
如图,已知AB∥CD,AE=CF,则下列条件中不一定能使△ABE≌△CDF的是( )| A、AB=CD |
| B、BE∥DF |
| C、∠B=∠D |
| D、BE=DF |
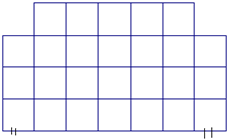 一展览馆有26间展室,图中每个方格代表一个展室,每相邻展室有门相同,出口、入口如图所示.问:能否找到一条从入口到出口的参观路线,使不重复不遗漏地走过每一间展室?
一展览馆有26间展室,图中每个方格代表一个展室,每相邻展室有门相同,出口、入口如图所示.问:能否找到一条从入口到出口的参观路线,使不重复不遗漏地走过每一间展室?