题目内容
4.化简求值:($\frac{4x+2}{{x}^{2}-1}$-$\frac{2}{x+1}$)÷$\frac{x+2}{{x}^{2}-2x+1}$,其中x=$\sqrt{2}$-1.分析 根据分式的运算法则即可求出答案.
解答 解:原式=$\frac{2(x+2)}{(x+1)(x-1)}•\frac{(x-1)^{2}}{x+2}$
=$\frac{2(x-1)}{x+1}$
当x=$\sqrt{2}$-1
∴原式=$\frac{2(\sqrt{2}-1-1)}{\sqrt{2}}$=2-2$\sqrt{2}$
点评 本题考查分式的化简求值,解题的关键是熟练运用分式的化简求值,本题属于基础题型.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
7.通讯员要在规定时间内到达某地,他每小时走15千米,则可提前24分钟到达某地;如果每小时走12千米,则要迟到15分钟.设通讯员到达某地的路程是x千米,原定的时间为y小时,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{\frac{x}{15}-15=y}\\{\frac{x}{12}+12=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{15}+15=y}\\{\frac{x}{12}-12=y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{15}-\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{15}+\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ |

 如图,在△ABC中,DE是AC的垂直平分线,点D在BC上,△ABC的周长为20cm,△ABD的周长为12cm,则AE的长为4cm.
如图,在△ABC中,DE是AC的垂直平分线,点D在BC上,△ABC的周长为20cm,△ABD的周长为12cm,则AE的长为4cm. 如图,已知△ABC,∠BAC=90°,AB=6,AC=8.
如图,已知△ABC,∠BAC=90°,AB=6,AC=8.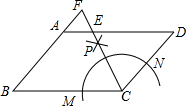 如图,在?ABCD中,AB=6,BC=8,以C为圆心适当长为半径画弧分别交BC,CD于M,N两点,分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,两弧在∠BCD的内部交于点P,连接CP并延长交AD于E,交BA的延长线于F,则AE+AF的值等于4.
如图,在?ABCD中,AB=6,BC=8,以C为圆心适当长为半径画弧分别交BC,CD于M,N两点,分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,两弧在∠BCD的内部交于点P,连接CP并延长交AD于E,交BA的延长线于F,则AE+AF的值等于4.