题目内容
4.在△ABC中,AD平分∠BAC,交BC于点D,过点D分别作DE∥AC,DF∥AB,分别交AB、AC于点E、F,说明AD与EF的位置关系.分析 由DE∥AC,DF∥AB得出四边形AEDF是平行四边形,进而得出∠DAF=∠ADE,由∠EAD=∠DAF得出∠ADE=∠EAD,AE=ED,于是得到四边形AEDF是菱形,最后得出结论.
解答  解:互相垂直平分,
解:互相垂直平分,
理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴∠DAF=∠ADE,
∵∠EAD=∠DAF,
∴∠ADE=∠EAD,
∴AE=ED,
∴四边形AEDF是菱形,
∴AD与EF互相垂直平分.
点评 本题主要考查了平行四边形的判定和性质,菱形的判定和性质,熟练掌握菱形的判定和性质是解决问题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
14.将一个平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法共有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 无数种 |
12.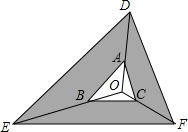 如图,点O是△ABC内一点、分别连接OA、OB、OC并延长到点D、E、F,使AD=2OA,BE=2OB,CF=2OC,连接DE,EF,FD.若△ABC的面积是3,则阴影部分的面积是( )
如图,点O是△ABC内一点、分别连接OA、OB、OC并延长到点D、E、F,使AD=2OA,BE=2OB,CF=2OC,连接DE,EF,FD.若△ABC的面积是3,则阴影部分的面积是( )
 如图,点O是△ABC内一点、分别连接OA、OB、OC并延长到点D、E、F,使AD=2OA,BE=2OB,CF=2OC,连接DE,EF,FD.若△ABC的面积是3,则阴影部分的面积是( )
如图,点O是△ABC内一点、分别连接OA、OB、OC并延长到点D、E、F,使AD=2OA,BE=2OB,CF=2OC,连接DE,EF,FD.若△ABC的面积是3,则阴影部分的面积是( )| A. | 6 | B. | 15 | C. | 24 | D. | 27 |
16.下列说法正确的是( )
(1)整式2xy-8x2y+8x3y因式分解的结果是2xy(1-4x+4x2);
(2)要使y=$\frac{\sqrt{3-x}}{x}$有意义,则x应该满足0<x≤3;
(3)“x的2倍与5的和”用代数式表示是一次式;
(4)地球上的陆地面积约为149000000平方千米,用科学记数法表示为1.49×108平方千米.
(1)整式2xy-8x2y+8x3y因式分解的结果是2xy(1-4x+4x2);
(2)要使y=$\frac{\sqrt{3-x}}{x}$有意义,则x应该满足0<x≤3;
(3)“x的2倍与5的和”用代数式表示是一次式;
(4)地球上的陆地面积约为149000000平方千米,用科学记数法表示为1.49×108平方千米.
| A. | (1)(4) | B. | (1)(2) | C. | (2)(3) | D. | (3)(4) |
13.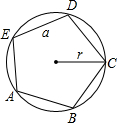 圆的内接正五边形ABCDE的边长为a,圆的半径为r.下列等式成立的是( )
圆的内接正五边形ABCDE的边长为a,圆的半径为r.下列等式成立的是( )
 圆的内接正五边形ABCDE的边长为a,圆的半径为r.下列等式成立的是( )
圆的内接正五边形ABCDE的边长为a,圆的半径为r.下列等式成立的是( )| A. | a=2rsin36° | B. | a=2rcos36° | C. | a=rsin36° | D. | a=2rsin72° |
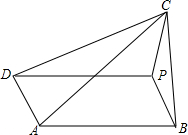 四边形ABCD内部存在一点P,使得ABPD为平行四边形.求证:若∠CBP=∠CDP,则∠ACD=∠BCP,反之亦然.
四边形ABCD内部存在一点P,使得ABPD为平行四边形.求证:若∠CBP=∠CDP,则∠ACD=∠BCP,反之亦然. 如图,AB是⊙O的直径,点C在⊙O上,直线AB与过点C的切线交于点E,连接BC,AC,过点O作OD∥BC与直线CE交于点D,连接DA.
如图,AB是⊙O的直径,点C在⊙O上,直线AB与过点C的切线交于点E,连接BC,AC,过点O作OD∥BC与直线CE交于点D,连接DA.