题目内容
14．
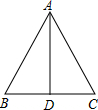等腰三角形的腰长为13，底为10．求它的面积．
分析 根据等腰三角形三线合一的性质可得BD=$\frac{1}{2}$BC，然后利用勾股定理列式求出AD，再根据三角形的面积公式列式计算即可得解．
解答 解：∵等腰三角形的腰长为13，底为10，
∴AB=AC=13，BC=10，AD是三角形ABC底边上的高，
∴BD=DC=$\frac{1}{2}$BC=5，
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12，
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×10×12=60．
点评 本题考查了等腰三角形三线合一的性质，勾股定理的应用，三角形的面积公式，熟记性质是解题的关键，根据图形解答更形象直观．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
一个大正方形和四个全等的小正方形按图①、图②两种方式摆放，根据图中数据，则图②的大正方形中未被小正方形覆盖部分的面积大小为24．
如图OP=1，过P作PP1⊥OP且PP1=1，得OP1=$\sqrt{2}$，再过点P1作P1P2⊥OP1且P1P2=1，连接OP2，得OP2=$\sqrt{3}$；又过点P2作P2P3⊥OP2且P2P3=1，得OP3=2；依此法继续作下去，得OP12+OP22+OP32+OP42+…+OPn2=$\frac{n（n+3）}{2}$．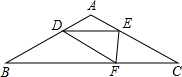
如图，在△ABC中，AB=AC=15，∠B=30°，点D为AB边上一动点，且AD=AE，BD=DF，要使△DEF与△CEF均为直角三角形，则AD的值为5或6．
如图，已知在△ABC中，CD⊥AB于D，BD=9，BC=15，AC=20．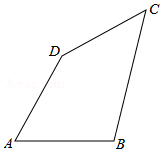
如图，在四边形ABCD中，AB=AD=8，∠A=60°，BC=10，CD=6．