题目内容
19. 如图,已知在△ABC中,CD⊥AB于D,BD=9,BC=15,AC=20.
如图,已知在△ABC中,CD⊥AB于D,BD=9,BC=15,AC=20.(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
分析 (1)在Rt△BCD中,根据勾股定理求出CD的长;
(2)在Rt△ACD中根据勾股定理求出AD的长,故可得出AB的长;
(3)由勾股定理的逆定理即可得出结论.
解答 (1)在△BCD中,因为CD⊥AB,
所以BD2+CD2=BC2.
所以CD2=BC2-BD2=152-92=144.
所以CD=12.
(2)在△ACD中,因为CD⊥AB,
所以CD2+AD2=AC2.
所以AD2=AC2-CD2=202-122=256.
所以AD=16.
所以AB=AD+BD=16+9=25.
(3)因为BC2+AC2=152+202=625,AB2=252=625,
所以AB2=BC2+AC2.
所以△ABC是直角三角形.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.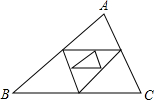 如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )
如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )
 如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )
如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )| A. | 22016 | B. | 22017 | C. | ${(\frac{1}{2})}^{2016}$ | D. | ${(\frac{1}{2})}^{2015}$ |
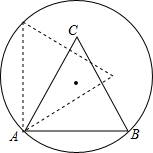 如图,正三角形ABC的边长为1,点A,B在半径为$\frac{\sqrt{2}}{2}$的圆上,点C在圆内,将正三角形ABC绕点A逆时针旋转,当点C第一次落在圆上时,则点C转过的度数为30°.
如图,正三角形ABC的边长为1,点A,B在半径为$\frac{\sqrt{2}}{2}$的圆上,点C在圆内,将正三角形ABC绕点A逆时针旋转,当点C第一次落在圆上时,则点C转过的度数为30°.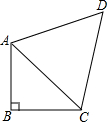 如图,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.
如图,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.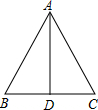 等腰三角形的腰长为13,底为10.求它的面积.
等腰三角形的腰长为13,底为10.求它的面积.
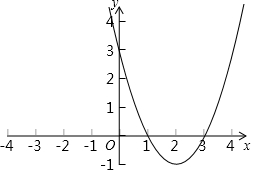 在平面直角坐标系xOy中,二次函数图象所在的位置如图所示:
在平面直角坐标系xOy中,二次函数图象所在的位置如图所示: