题目内容
2. 如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2=$\frac{n(n+3)}{2}$.
如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2=$\frac{n(n+3)}{2}$.
分析 根据勾股定理分别求出每个直角三角形斜边长,根据结果得出规律,即可得出答案.
解答 解:∵OP1=$\sqrt{2}$,
由勾股定理得:OP2=$\sqrt{(\sqrt{2})^{2}+{1}^{2}}$=$\sqrt{3}$,
OP3=$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=$\sqrt{4}$,
…
OPn=$\sqrt{n+1}$,
∴OP12+OP22+OP32+OP42+…+OPn2=2+3+4+5+…+n+1=$\frac{n(n+3)}{2}$.
故答案为:$\frac{n(n+3)}{2}$.
点评 本题考查了勾股定理的应用,注意:在直角三角形中,两直角边的平方和等于斜边的平方,解此题的关键是能根据求出的结果得出规律.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4.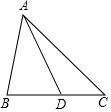 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )| A. | AB2=BC•BD | B. | AB2=AC•BD | C. | AB•AD=BD•BC | D. | AB•AC=BC•BD |
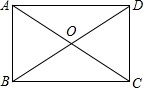 如图所示,矩形ABCD中,对角线AC、BD相交于O,∠ADB=30°,BD=6cm,试求此矩形的周长和面积.
如图所示,矩形ABCD中,对角线AC、BD相交于O,∠ADB=30°,BD=6cm,试求此矩形的周长和面积.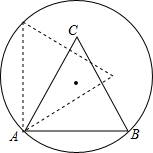 如图,正三角形ABC的边长为1,点A,B在半径为$\frac{\sqrt{2}}{2}$的圆上,点C在圆内,将正三角形ABC绕点A逆时针旋转,当点C第一次落在圆上时,则点C转过的度数为30°.
如图,正三角形ABC的边长为1,点A,B在半径为$\frac{\sqrt{2}}{2}$的圆上,点C在圆内,将正三角形ABC绕点A逆时针旋转,当点C第一次落在圆上时,则点C转过的度数为30°.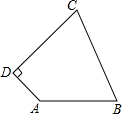 如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.
如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.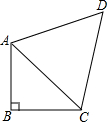 如图,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.
如图,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.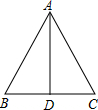 等腰三角形的腰长为13,底为10.求它的面积.
等腰三角形的腰长为13,底为10.求它的面积.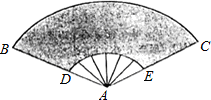 如图,扇形纸扇完全打开后,阴影部分为贴纸,外侧两竹条AB,AC的夹角为120°,弧BC的长为30πcm,AD的长为15cm,则贴纸的面积等于600πcm2.
如图,扇形纸扇完全打开后,阴影部分为贴纸,外侧两竹条AB,AC的夹角为120°,弧BC的长为30πcm,AD的长为15cm,则贴纸的面积等于600πcm2.