题目内容
3.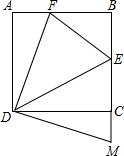 如图,正方形ABCD的边长为6,点E是BC的中点,点F在AB边上,BF=2AF,延长BC至点M,使得CM=AF.
如图,正方形ABCD的边长为6,点E是BC的中点,点F在AB边上,BF=2AF,延长BC至点M,使得CM=AF.(1)试判断FD和DM的位置和大小关系,并说明理由;
(2)求∠EDF的度数.
分析 (1)根据正方形的性质得AD=CD,∠A=∠BCD=∠ADC=90°,则利用“SAS”判定△ADF≌△CDM,所以FD=MD,∠ADF=∠CDM,则可计算出∠FDM=90°,于是可判断FD⊥DM;
(2)先计算出BE=CE=3,BF=4,AF=2,则CM=AF=2,EM=EC+CM=5,再利用勾股定理计算出EF=5,则可根据“SSS”判定△DEF≌△DEM,得到∠EDF=∠EDM,所以∠EDF=$\frac{1}{2}$∠FDM=45°.
解答 解:(1)FD=DM,FD⊥DM.理由如下:
∵四边形ABCD为正方形,
∴AD=CD,∠A=∠BCD=∠ADC=90°,
在△ADF和△CDM中
$\left\{\begin{array}{l}{AD=CD}\\{∠A=∠DCM}\\{AD=CM}\end{array}\right.$,
∴△ADF≌△CDM,
∴FD=MD,∠ADF=∠CDM,
∴∠FDM=∠FDC+∠CDM=∠FDC+∠ADF=90°,
∴FD⊥DM;
(2)∵点E是BC的中点,
∴BE=CE=3,
∵BF=2AF,AB=6,
∴BF=4,AF=2,
∴CM=AF=2,
∴EM=EC+CM=5,
在△BEF中,EF=$\sqrt{B{E}^{2}+B{F}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴EF=EM,
在△DEF和△DEM中
$\left\{\begin{array}{l}{DE=DE}\\{EF=EM}\\{DF=DM}\end{array}\right.$,
∴△DEF≌△DEM,
∴∠EDF=∠EDM,
∴∠EDF=$\frac{1}{2}$∠FDM=$\frac{1}{2}$×90°=45°.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了全等三角形的判定与性质.

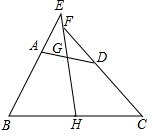 如图,四边形ABCD中,G,H分别是AD,BC的中点,AB=CD,BA,CD的延长线交HG的延长线于点E,F,求证:∠BEH=∠CFH.
如图,四边形ABCD中,G,H分别是AD,BC的中点,AB=CD,BA,CD的延长线交HG的延长线于点E,F,求证:∠BEH=∠CFH.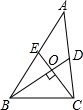 如图,已知BD,CE分别是△ABC的两条中线,BD⊥CE于点O,且CE=6,BD=8,则△ABC的面积为32.
如图,已知BD,CE分别是△ABC的两条中线,BD⊥CE于点O,且CE=6,BD=8,则△ABC的面积为32.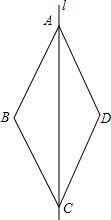 如图,直线l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AD=DC.其中正确的结论是①②④.
如图,直线l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AD=DC.其中正确的结论是①②④.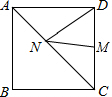 如图,在边长2正方形ABCD中,点M是CD的中点,在AC上确定点N,使DN+MN最小值是$\sqrt{5}$.
如图,在边长2正方形ABCD中,点M是CD的中点,在AC上确定点N,使DN+MN最小值是$\sqrt{5}$.