题目内容
7.解不等式组:$\left\{\begin{array}{l}{x+1≥3}\\{3(x-2)<x+4}\end{array}\right.$.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式x+1≥3,得:x≥2,
解不等式3(x-2)<x+4,得:x<5,
故不等式组的解集为:2≤x<5.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
2.下面各整式能直接运用完全平方公式分解因式的是( )
| A. | x2-x+1 | B. | x2+2x-1 | C. | -2x+x2+1 | D. | 2x-x2+1 |
12.给出四个数0,$\sqrt{3}$,π,-1,其中最小的是( )
| A. | 0 | B. | $\sqrt{3}$ | C. | π | D. | -1 |
16.若$\frac{{\sqrt{2x-1}}}{x-3}$在实数范围内有意义,则x的取值范围是( )
| A. | x≠3 | B. | x>$\frac{1}{2}$且x≠3 | C. | x≥2 | D. | x≥$\frac{1}{2}$且x≠3 |
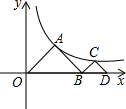 如图,△AOB,△CBD是等腰直角三角形,点A、C在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OB,BD都在x轴上,则点D的横坐标是4$\sqrt{2}$.
如图,△AOB,△CBD是等腰直角三角形,点A、C在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OB,BD都在x轴上,则点D的横坐标是4$\sqrt{2}$.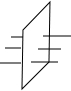 如图,有红、黄、蓝粗细均匀的木棍各一根分别穿过木板,甲乙两人在木板的两侧同时随机抓住一根木棍,则他们抓住的木棍颜色相同的概率是$\frac{1}{3}$.
如图,有红、黄、蓝粗细均匀的木棍各一根分别穿过木板,甲乙两人在木板的两侧同时随机抓住一根木棍,则他们抓住的木棍颜色相同的概率是$\frac{1}{3}$.