题目内容
12.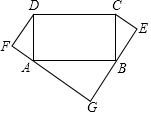 如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△CBE,延长FA、EB交于点G.
如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△CBE,延长FA、EB交于点G.(1)求证:△ADF∽△BAG;
(2)若DF=4,请连接EF并求出EF的长.
分析 (1)易证∠DAF=∠GBA和∠ADF=∠BAG即可解题;
(2)连接EF,根据(1)结论可以求得AG,BG的长度,易证△ABG为Rt△,即可解题.
解答 解:(1)∵四边形ABCD为矩形,
∴∠DAB=90°,即∠DAF+∠BAG=90°,
又∵∠DAF+∠ADF=90°,
∴∠ADF=∠BAG,
同理∠ECB=∠GBA,
∵△ADF≌△CBE,
∴∠ECB=∠DAF,
∴∠DAF=∠GBA,
∵在△ADF和△BAG中,$\left\{\begin{array}{l}{∠DAF=∠GBA}\\{∠ADF=∠BAG}\end{array}\right.$,
∴△ADF∽△BAG;
(2)连接EF,如图,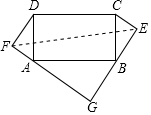
∵在Rt△ADF中,AD=5,DF=4,∴AF=$\sqrt{{AD}^{2}{-DF}^{2}}$=3,
∵△ADF∽△BAG,
∴$\frac{AD}{AB}$=$\frac{DF}{AG}$=$\frac{AF}{GB}$,∠AGB=∠AFD=90°,
∴AG=8,BG=6,
∴FG=AF+AG=11,EG=EB+BG=DF+BG=4+6=10,
∴在Rt△EFG中,EF=$\sqrt{{FG}^{2}{+EG}^{2}}$=$\sqrt{221}$.
点评 本题考查了相似三角形的判定和相似三角形对应边比例相等的性质,考查了全等三角形对应边、对应角相等的性质,本题中求证∠AGB是直角是解题的关键.

练习册系列答案
相关题目
3. 某住宅小区六月份1日至6日每天用水量变化情况如折线图所示,那么这6天的平均用水量是( )
某住宅小区六月份1日至6日每天用水量变化情况如折线图所示,那么这6天的平均用水量是( )
 某住宅小区六月份1日至6日每天用水量变化情况如折线图所示,那么这6天的平均用水量是( )
某住宅小区六月份1日至6日每天用水量变化情况如折线图所示,那么这6天的平均用水量是( )| A. | 30吨 | B. | 31 吨 | C. | 32吨 | D. | 33吨 |
 如图,在正方形网格有△ABC,每个方格的长度为一个单位长度,
如图,在正方形网格有△ABC,每个方格的长度为一个单位长度,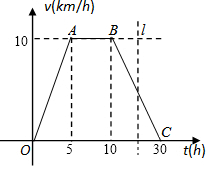 据环保中心观察和预测:发生于甲地的河流污染一直向下游方向移动,其移动速度v(千米/小时)与时间t(小时)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(小时)内污染所经过的路程S(千米).
据环保中心观察和预测:发生于甲地的河流污染一直向下游方向移动,其移动速度v(千米/小时)与时间t(小时)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(小时)内污染所经过的路程S(千米). 如图,两个扇形半径均为1,α=120°,β=60°,则大扇形与小扇形的面积之差为$\frac{π}{6}$.
如图,两个扇形半径均为1,α=120°,β=60°,则大扇形与小扇形的面积之差为$\frac{π}{6}$. 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上,以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是(4,2)或(-4,-2).
如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上,以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是(4,2)或(-4,-2).