题目内容
20. 如图,在正方形网格有△ABC,每个方格的长度为一个单位长度,
如图,在正方形网格有△ABC,每个方格的长度为一个单位长度,(1)作出与△ABC关于y轴对称的图形.
(2)求出△ABC的面积.
分析 (1)直接利用关于y轴对称点的性质分别得出对应点位置进而得出答案;
(2)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案.
解答  解:(1)如图所示:△ABC关于y轴对称的图形为△DEF;
解:(1)如图所示:△ABC关于y轴对称的图形为△DEF;
(2)△ABC的面积为:4×5-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×5-$\frac{1}{2}$×4×4=8.
点评 此题主要考查了三角形面积求法以及轴对称变换,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
15.下列函数是二次函数的有( )
(1)y=1-x2;(2)y=$\frac{2}{{x}^{2}}$;(3)y=x(x-3);(4)y=ax2+bx+c;(5)y=2x+1;(6)y=2(x+3)2-2x2.
(1)y=1-x2;(2)y=$\frac{2}{{x}^{2}}$;(3)y=x(x-3);(4)y=ax2+bx+c;(5)y=2x+1;(6)y=2(x+3)2-2x2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.下列方程是二元一次方程的是( )
| A. | 2x-xy=5 | B. | $\frac{x}{2}$+3y=1 | C. | x+$\frac{1}{y}$=2 | D. | x2-2y=0 |
10.“服务他人,提升自我”,某学校积极开展志愿者服务活动,来自初三的5名同学(3男3女)成立了“交通秩序维护”小分队,若从该小分队中任选两名同学进行交通秩序维护,则恰好是一男一女的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
 如图,抛物线y=ax2+bx+2经过点A(-1,0),B(4,0),交y轴于点C;
如图,抛物线y=ax2+bx+2经过点A(-1,0),B(4,0),交y轴于点C;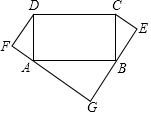 如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△CBE,延长FA、EB交于点G.
如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△CBE,延长FA、EB交于点G.