Question

17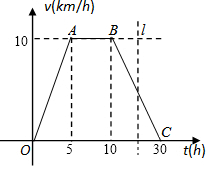．据环保中心观察和预测：发生于甲地的河流污染一直向下游方向移动，其移动速度v（千米/小时）与时间t（小时）的函数图象如图所示，过线段OC上一点T（t，0）作横轴的垂线l，梯形OABC在直线l左侧部分的面积即为t（小时）内污染所经过的路程S（千米）．
（1）当t=3时，求s的值；
（2）将s随t变化的规律用数学关系式表示出来（t≤30）；
（3）若乙城位于甲地的下游，且距甲地174km，试判断这河流污染是否会侵袭到乙城，如果会，在河流污染发生后多长时间它将侵袭到乙城？如果不会，请说明理由．

Answer 1

分析 （1）求出直线OA的解析式即可解决问题；
（2）分三个时间段分别求解即可；
（3）分三个时间段分别求解即可解决问题；

解答 解：（1）由图象可知：直线OA的解析式为v=2t，
当t=3时，v=2×3=6，
所以s=$\frac{1}{2}$×2×6=6．

（2）当0≤t≤5时，s=$\frac{1}{2}$•t•2t=t²； 
当5＜t≤10时，s=$\frac{1}{2}$×5×10+10（t-5）=10t-25；        
当10＜t≤30时，s=$\frac{1}{2}$×5×10+10×5+（t-10）×10-$\frac{1}{2}$×（t-10）×$\frac{1}{2}$（t-10）
=-$\frac{1}{4}$t²+15t-50．
综上可知s=$\left\{\begin{array}{l}{{t}^{2}}&{（0≤t≤5）}\\{10t-25}&{（5＜t≤10）}\\{-\frac{1}{4}{t}^{2}+15t-50}&{（10＜t≤30）}\end{array}\right.$，
（3）当0≤t≤5时，S_最大值=5²=25＜174．
当5＜t≤10时，S_最大值=10×10-25=75＜174．
当10＜t≤30时，令-$\frac{1}{4}$t²+15t-50=174，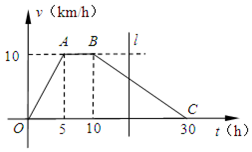

解得t₁=28，t₂=32，10＜t≤30，故t=28，
所以河流污染发生28h后将侵袭到乙城．

点评 本题考查一次函数的应用、待定系数法等知识，分段函数等知识，解题的关键是读懂图象信息，灵活运用所学知识解决问题．